CHƯƠNG 4   

    LÝ THUYẾT VỀ HÀNH VI CỦA NHÀ SẢN XUẤT  

PHẦN I             LÝ THUYẾT SẢN XUẤT

I. SẢN XUẤT LÀ GÌ? 

1. YẾU TỐ ĐẦU VÀO VÀ YẾU TỐ ĐẦU RA  
2. CÔNG NGHỆ

3. HÀM SẢN XUẤT  

II.  NĂNG SUẤT BIÊN VÀ NĂNG SUẤT TRUNG BÌNH  

1. NĂNG SUẤT BIÊN  

2. QUY LUẬT NĂNG SUẤT BIÊN GIẢM DẦN

3. NĂNG SUẤT TRUNG BÌNH  

4. ĐỒ THỊ ĐƯỜNG TỔNG SẢN LƯỢNG, ĐƯỜNG NĂNG SUẤT BIÊN VÀ ĐƯỜNG     NĂNG SUẤT TRUNG BÌNH

5. TÁC ĐỘNG CỦA TIẾN BỘ CÔNG NGHỆ ĐẾN SẢN LƯỢNG  

III.   ĐƯỜNG ĐẲNG LƯỢNG

1. ĐƯỜNG ĐẲNG LƯỢNG  

2. TỶ LỆ THAY THẾ KĨ THUẬT CON

3. MỐI QUAN HỆ GIỮA TỶ LỆ THAY THẾ KỸ THUẬT BIÊN VÀ NĂNG SUẤT BIÊN

IV. MỘT SỐ HÀM SẢN XUẤT THÔNG DỤNG VÀ ĐƯỜNG ĐẲNG LƯỢNG TƯƠNG  ỨNG

1. HÀM SẢN XUẤT TUYẾN TÍNH  

2. HÀM SẢN XUẤT VỚI TỶ LỆ KẾT HỢP CỐ ĐỊNH

3.   HÀM SẢN XUẤT COBB-DOUGLAS

V.  HIỆU SUẤT THEO QUY MÔ

VI. ĐƯỜNG ĐẲNG PHÍ

VII.  NGUYÊN TẮC TỐI ĐA HÓA SẢN LƯỢNG HAY TỐI THIỂU HÓA CHI PHÍ  

1. NGUYÊN TẮC TỐI ĐA HÓA SẢN LƯỢNG

2. NGUYÊN TẮC TỐI THIỂU HÓA CHI PHÍ SẢN XUẤT

PHẦN II 

LÝ THUYẾT VỀ CHI PHÍ SẢN XUẤT

I. CHI PHÍ KẾ TÓAN VÀ CHI PHÍ CƠ HỘI  

II. CHI PHÍ NGẮN HẠN  

1. TỔNG CHI PHÍ, CHI PHÍ CỐ ĐỊNH VÀ CHI PHÍ BIẾN ĐỔI

2. CHI PHÍ TRUNG BÌNH (AC) VÀ CHI PHÍ BIÊN (MC)  

3. HÌNH DẠNG CỦA ĐƯỜNG CHI PHÍ BIÊN

4. MỐI QUAN HỆ GIỮA CHI PHÍ TRUNG BÌNH VÀ CHI PHÍ BIÊN  

III. CHI PHÍ DÀI HẠN

1. TỔNG CHI PHÍ DÀI HẠN
2. CHI PHÍ TRUNG BÌNH VÀ CHI PHÍ BIÊN

IV.  TÍNH KINH TẾ THEO QUY MÔ  

PHẦN III

TỐI ĐA HÓA LỢI NHUẬN

VÀ QUYẾT ĐỊNH CUNG CỦA DOANH NGHIỆP  

I. TỐI ƯU HÓA LỢI NHUẬN

1. DOANH THU BIÊN

2. NGUYÊN TẮC TỐI ĐA HÓA LỢI NHUẬN

II. QUYẾT ĐỊNH CUNG CỦA DOANH NGHIỆP

1. QUYẾT ĐỊNH CUNG TRONG NGẮN HẠN
2. QUYẾT ĐỊNH CUNG TRONG DÀI HẠN

III. NGUYÊN TẮC TỐI ĐA HÓA TRONG DOANH THU

IV. TỐI ĐA HÓA LỢI NHUẬN VỚI CÁC YẾU TỐ ĐẦU VÀO

CÂU HỎI THẢO LUẬN

BÀI TẬP

MỘT SỐ THUẬT NGỮ

 Chương 4

    LÝ THUYẾT VỀ HÀNH VI CỦA NHÀ SẢN XUẤT

Trong chương này, chúng tôi trình bày ba nội cơ bản của lý thuyết về hành vi của nhà sản xuất. Ba nội dung cơ bản này là lý thuyết sản xuất, lý thuyết chi phí sản xuất và lý thuyết về sự tối đa hóa lợi nhuận của nhà sản xuất.

  PHẦN I. LÝ THUYẾT SẢN XUẤT

    Sau khi đã phân tích các vấn đề về khía cạnh cầu trong chương trước, bây giờ chúng ta chuyển sang các vấn đề về cung mà đại diện cho nó là các nhà sản xuất hay các doanh nghiệp. Làm thế nào mà các doanh nghiệp quyết định được phải sử dụng bao nhiêu lao động, máy móc thiết bị, nguyên vật liệu, sản xuất bao nhiêu sản phẩm và nên bán với giá bao nhiêu? Lý thuyết về cung sẽ cho ta biết về các vấn đề đó.

Chương này nghiên cứu hành vi sản xuất - kinh doanh của doanh nghiệp nhằm giải quyết mối quan hệ giữa sản lượng, chi phí và lợi nhuận. Nói cách khác, chúng ta sẽ nghiên cứu cách thức các doanh nghiệp quyết định sản lượng và tính toán các chi phí để thu được lợi nhuận tối đa.

      Sản xuất là hoạt động tạo ra sản phẩm của các doanh nghiệp nhằm đáp ứng nhu cầu của người tiêu dùng. Nói cách khác, sản xuất là quá trình chuyển hóa các yếu tố đầu vào thành các yếu tố đầu ra (hay là sản phẩm).

  Yếu tố đầu vào hay còn gọi là yếu tố sản xuất là bất kỳ hàng hóa hay dịch vụ nào được dùng để sản xuất ra hàng hóa, dịch vụ khác. Yếu tố đầu vào bao gồm lao động, máy móc thiết bị, nhà xưởng, nguyên vật liệu, năng lượng, v.v. Hàng hóa và dịch vụ là những đầu ra của sản xuất.

Thí dụ, Công ty Coca Cola sử dụng các yếu tố đầu vào là lao động, máy móc thiết bị, nước, gaz, đường, v.v. để sản xuất ra nước giải khát. Lao động ở đây có thể được hiểu là thời gian làm việc của người vận hành máy móc, nhà quản lý, công nhân v.v. Các yếu tố sản xuất khác được gọi chung là vốn như: nguyên vật liệu, máy móc, thiết bị, nhà xưởng, v.v. Chúng ta có thể thấy rằng mỗi quá trình sản xuất cụ thể sẽ cần những yếu tố đầu vào riêng của chúng. Chẳng hạn, yếu tố đầu vào của một buổi hòa nhạc là thời gian làm việc của người biểu diễn, kỹ thuật viên âm thanh, nhà quản lý nhà hát và những người có liên quan, các thiết bị âm thanh, v.v. Để sản xuất ra lúa gạo, chúng ta cần có nước, phân, lao động, giống, v.v. Vì vậy, để nghiên cứu một quá trình sản xuất tổng quát, chúng ta có thể chia các đầu vào, theo tiêu thức chung nhất của mọi quá trình sản xuất, thành lao động và vốn. Chúng ta nên lưu ý rằng công nghệ sản xuất ra một sản phẩm nào đó không thuộc phạm vi nghiên cứu của kinh tế học mà là đối tượng của các nhà kỹ thuật. Các nhà kinh tế chỉ quan tâm đến hiệu quả của việc sản xuất ở một trình độ công nghệ nhất định.

      Mối quan hệ giữa yếu tố đầu vào và đầu ra được quyết định bởi kỹ thuật sản xuất hay còn gọi là công nghệ. Công nghệ là cách thức sản xuất ra hàng hóa, dịch vụ. Công nghệ được cải tiến khi có những phát minh khoa học mới được áp dụng trong sản xuất. Công nghệ tiến bộ sẽ dẫn đến những phương pháp sản xuất mới mà chúng có thể sử dụng tài nguyên hiệu quả hơn. Điều này có nghĩa là những công nghệ mới có thể sản xuất ra nhiều sản phẩm hơn với cùng số lượng các yếu tố đầu vào như trước hay thậm chí ít hơn. Với những công nghệ mới, máy móc thiết bị có năng suất cao hơn và công nhân có thể đạt năng suất cao hơn. Những điều này làm tăng năng lực sản xuất của nền kinh tế.

      Mối quan hệ giữa số lượng các yếu tố đầu vào và số lượng đầu ra (sản phẩm) làm ra của quá trình sản xuất được biểu diễn bằng hàm sản xuất.  Hàm sản xuất của một loại sản phẩm nào đó cho biết số lượng sản phẩm tối đa của sản phẩm đó (ký hiệu là q) có thể được sản xuất ra bằng cách sử dụng các phối hợp khác nhau của vốn (K) và lao động (L), với một trình độ công nghệ nhất định. Vì thế, hàm sản xuất thông thường được viết như sau:

                                                                                                                (4.1)

   trong đó: q là số lượng sản phẩm tối đa có thể được sản xuất ra ở một trình độ công nghệ nhất định ứng với các kết hợp của các yếu tố đầu vào là lao động (L) và vốn (K) khác nhau. Hàm sản xuất chỉ có ý nghĩa đối với những giá trị không âm của K và L. Thông thường hàm sản xuất được giả định là hàm số đồng biến với vốn và lao động, nghĩa là  và  trong miền xác định của hàm số sản xuất vì trong một chừng mực nhất định, khi sử dụng nhiều yếu tố đầu vào hơn, nhà sản xuất sẽ sản xuất ra nhiều sản phẩm hơn.

Số lượng sản phẩm q sản xuất ra thay đổi tùy thuộc vào sự thay đổi của số lượng vốn và lao động. Hàm sản xuất trong phương trình (4.1) áp dụng cho một trình độ công nghệ nhất định. Một hàm số f cụ thể có thể đặc trưng cho một trình độ công nghệ nhất định. Khi công nghệ thay đổi thì hàm sản xuất sẽ thay đổi và số lượng sản phẩm sản xuất ra sẽ lớn hơn với cùng số lượng các yếu tố như trước hay thậm chí ít hơn.

Như ta đã biết, hàm sản xuất mô tả mối quan hệ giữa số lượng của các yếu tố đầu vào (vốn và lao động) và sản lượng đầu ra. Thí dụ, hàm sản xuất có thể biểu diễn sản lượng lúa mà một nông dân có thể thu hoạch được với một số lượng lao động và diện tích đất đai, phân bón, thuốc trừ sâu nhất định; hàm sản xuất mô tả số lượng áo quần do một xưởng may sản xuất ra trong, chẳng hạn, một tuần khi sử dụng một số lượng lao động và máy móc thiết bị nào đó.

      Để xem xét tác động của một yếu tố sản xuất nào đó đến sản lượng, chúng ta khảo sát sự thay đổi của sản lượng khi số lượng yếu tố sản xuất đó thay đổi trong khi các yếu tố sản xuất khác giữ nguyên. Bây giờ, chúng ta hãy xét ảnh hưởng của lao động (hay vốn) đến sản lượng đầu ra khi số lượng lao động (hay vốn) được sử dụng trong sản xuất thay đổi trong khi số vốn (hay lao động) không đổi. Khi xem xét tác động này, ta có các khái niệm về năng suất biên và trung bình.

      Trước hết, chúng ta hãy phân tích quá trình sản xuất lúa của một nông dân. Để sản xuất ra lúa, giả sử người nông dân cần hai yếu tố đầu vào chủ yếu là đất đai và lao động. Giả sử anh ta có một diện tích đất và các công cụ sản xuất cố định nhưng anh ta có thể thuê nhiều hay ít lao động tùy theo điều kiện sản xuất.

Bảng 4.1 mô tả mối quan hệ giữa số lượng các yếu tố đầu vào và sản lượng lúa của quá trình sản xuất này. Diện tích đất đai được giữ cố định ở một đơn vị (1 hecta chẳng hạn) và số lượng lao động được sử dụng trong sản xuất tăng dần từ 1 đến 10. Rõ ràng, nếu không có lao động nào thì quá trình sản xuất không diễn ra và sản lượng sẽ bằng không. Khi bắt đầu sử dụng một lao động, sản lượng tăng lên 3 đơn vị; ta nói năng suất biên của người lao động thứ nhất là 3. Khi tăng số lao động lên 2, sản lượng tăng từ 3 lên 7 đơn vị; ta nói năng suất biên của lao động thứ hai này là 4. Tương tự, khảo sát sự thay đổi của sản lượng khi tăng dần số lao động, chúng ta có thể hình thành cột năng suất biên của lao động. Đó là cột 4 trong bảng 4.1.

Năng suất biên của một yếu tố sản xuất nào đó (vốn hay lao động) là lượng sản phẩm tăng thêm được sản xuất ra do sử dụng thêm một đơn vị yếu tố sản xuất đó. Như vậy, năng suất biên của vốn và lao động có thể được tính lần lượt như sau:

  ,                                                                                            (4.2)

  ,                                                                                               (4.3)

  trong đó: MPK và MPL lần lượt là năng suất biên của vốn và lao động.

  Bảng 4.1. Mối quan hệ giữa yếu tố đầu vào và đầu ra của sản xuất lúa

            Như vậy, năng suất biên của một yếu tố sản xuất nào đó chính là đạo hàm của tổng sản lượng theo số lượng yếu tố sản xuất đó. Như vậy, về mặt hình học, năng suất biên là độ dốc của đường tiếp tuyến của đồ thị hàm sản xuất tại từng điểm cụ thể.

      Quan sát sự biến đổi của năng suất biên khi số lao động tăng lên, chúng ta nhận thấy năng suất biên lúc đầu tăng lên nhưng khi số lao động từ 4 trở lên năng suất biên lại có xu hướng giảm dần.

Chúng ta hãy tìm hiểu xem tại sao lại có sự giảm dần này trong quá trình sản xuất. Với diện tích đất đai là 1 ha, người lao động đầu tiên có cả diện tích đất và công cụ để làm việc. Anh ta có rất nhiều công việc để làm và có thể diện tích đó là quá sức đối với anh ta. Với sự giúp đỡ của người thứ hai hay người thứ ba, mọi người sẽ sản xuất ra nhiều hơn, năng suất biên của những người này tăng dần. Với 3 lao động, diện tích đất có thể vừa đủ để mọi người làm việc hết sức mình và mỗi người chuyên tâm làm công việc theo kỹ năng của mình chẳng hạn như: cắt lúa, vận chuyển và phơi. Khi số lao động tăng lên 4, diện tích đất cũng như số công cụ lao động phải được chia sẻ cho mỗi người và họ sẽ không làm việc hết khả năng của mình. Sản lượng sẽ tăng chậm hơn và năng suất biên của người thứ tư giảm xuống. Rõ ràng khi thêm nhiều lao động thì mỗi lao động chỉ có ít vốn và diện tích để làm việc, thời gian “chết” nhiều hơn và mỗi người khó có thể làm việc theo khả năng của mình nên năng suất biên cứ giảm dần. Cho đến người thứ tám, công việc của người này có thể là mang nước uống cho những người khác nên hầu như sản lượng không tăng lên nữa và năng suất biên của anh ta bằng không. Ở những mức lao động cao hơn, tình trạng lãng công có thể xảy ra nên sản lượng có thể giảm sút. Năng suất biên có thể âm.

            Đối với hầu hết các quá trình sản xuất, năng suất biên của các yếu tố sản xuất (vốn và lao động) cũng diễn biến theo quá trình tương tự. Do vậy, quy luật năng suất biên giảm dần có thể được phát biểu như sau:

"Nếu số lượng của một yếu tố sản xuất tăng dần trong khi số lượng (các) yếu tố sản xuất khác giữ nguyên thì sản lượng sẽ gia tăng nhanh dần. Tuy nhiên, vượt qua một mốc nào đó thì sản lượng sẽ gia tăng chậm hơn. Nếu tiếp tục gia tăng số lượng yếu tố sản xuất đó thì tổng sản lượng đạt đến mức tối đa và sau đó sẽ sút giảm."

Trong phân tích sản xuất, chúng ta giả định rằng tất cả các yếu tố đầu vào đều có chất lượng như nhau. Năng suất biên giảm dần là kết quả của những hạn chế khi sử dụng các đầu vào cố định khác (như máy móc, thiết bị chẳng hạn).

Quy luật năng suất biên giảm dần tác động đến hành vi và quyết định của doanh nghiệp trong việc lựa chọn các yếu tố đầu vào như thế nào để tăng năng suất, giảm chi phí và tối đa hóa lợi nhuận.

  Cột thứ năm của bảng 4.1 mô tả năng suất trung bình của lao động, tức là sản lượng tính trên mỗi đơn vị lao động. Năng suất trung bình của một yếu tố sản xuất nào đó được tính bằng cách lấy tổng sản lượng chia cho số lượng yếu tố sản xuất đó. Ta có thể tính năng suất lao động trung bình và năng suất vốn trung bình theo các công thức sau:

  ,                                                                                                                (4.4)

                        ,                                                                                                      (4.5)

trong đó: APL và APK lần lượt là năng suất trung bình của lao động và của vốn.           

Trong thí dụ trên, năng suất trung bình của lao động lúc đầu cũng tăng lên nhưng sau đó giảm đi khi số lao động từ 4 trở lên. Chúng ta có thể nhận thấy năng suất trung bình của lao động giảm xuống khi năng suất biên thấp hơn năng suất trung bình. Ngược lại, năng suất trung bình tăng lên khi năng suất biên lớn hơn năng suất trung bình.

 Từ bảng 4.1, chúng ta có thể xây dựng hình dạng của các đường tổng sản lượng, đường năng suất biên và năng suất trung bình của lao động như hình 4.1.

Đường tổng sản lượng, đường năng suất biên và đường năng suất trung bình có mối quan hệ chặt chẽ với nhau. Vì năng suất biên là đạo hàm của tổng sản lượng nên về mặt hình học, nó là độ dốc của đường tổng sản lượng. Ở những mức lao động đầu tiên, tổng sản lượng tăng rất nhanh nên độ dốc của đường này tăng và như vậy năng suất biên tăng, đường năng suất biên dốc lên. Khi số lao động lớn hơn 3, tổng sản lượng tăng chậm dần, độ dốc của đường sản lượng giảm nên năng suất biên giảm. Đường năng suất biên dốc xuống. Sau đó, đường sản lượng đạt cực đại, điều này cũng có nghĩa là việc tăng thêm số lao động không làm tăng thêm sản lượng. Vì vậy, lúc này, năng suất biên sẽ bằng không. Đường năng suất biên cắt trục hoành. Sau đó, sản lượng giảm xuống, đường tổng sản lượng có độ dốc âm nên năng suất biên âm.

Đối với đường năng suất lao động trung bình: Trên đồ thị 4.1, ta thấy đường năng suất lao động trung bình cắt đường năng suất lao động biên tại điểm có hoành độ là L₂. Tại điểm này, năng suất lao động trung bình đạt cực đại.

            Trên đường tổng sản lượng q, ta có thể chọn một điểm bất kỳ và kẻ một đường thẳng bất kỳ từ gốc tọa độ đến điểm này. Ta có thể chứng minh được một cách dễ dàng là năng suất lao động trung bình của số lao động ứng với điểm này sẽ chính là độ dốc của đường thẳng này. Tại điểm ứng với số lượng lao động là L₂, đường kẻ từ gốc tọa độ sẽ tiếp xúc với đường tổng sản lượng. Như thế, tại đây năng suất lao động trung bình sẽ bằng với năng suất lao động biên. Với số lao động thấp hơn mức L₂, độ dốc của đường thẳng kẻ từ gốc tọa độ sẽ nhỏ hơn độ dốc của đường q nên AP < MP. Khi đó, năng suất trung bình sẽ tăng lên nếu ta gia tăng số lượng lao động. Thí dụ, giả sử một lao động duy nhất của một nông trang có thể cắt được 1 công lúa một ngày, năng suất trung bình của người này cũng là 1 công/ngày/người. Khi thuê thêm một lao động nữa, cả hai người cắt được 3 công lúa một ngày nên năng suất biên của người thứ hai là hai, cao hơn năng suất trung bình của người thứ nhất nên sẽ làm năng suất trung bình của cả hai người tăng lên, đó là, 1,5 công/ngày/người.

Cũng giống như thế, đối với các điểm phía phải của điểm L₂, thì AP > MP, và do vậy năng suất trung bình giảm dần khi ta sử dụng thêm lao động. Thí dụ, giả sử người chủ nông trại thuê thêm người thứ 3, người này có năng suất biên là 1 công, thấp hơn năng suất trung bình của hai người ban đầu. Do đó, năng suất trung bình của ba người giảm xuống còn 1,33.

Như vậy, tại điểm năng suất lao động trung bình bằng với năng suất lao động biên thì năng suất lao động trung bình là cực đại. Chúng ta có thể chứng minh nhận xét này qua hàm sản xuất sau.

Thí dụ: Giả sử ta có hàm sản xuất có dạng như sau:

.

Để xây dựng hàm số năng suất lao động trung bình, hàm số năng suất lao động biên, ta cố định giá trị K bằng cách cho K = K₀ = 10 chẳng hạn.   

            Khi đó, hàm số sản xuất trở thành:

(1)   Năng suất lao động biên:

.

Kết quả này cho chúng ta thấy đường năng suất lao động biên có dạng hình chữ U lật úp như đã vẽ ở trước.

(2)   Năng suất lao động trung bình:

.

Đường năng suất lao động trung bình cũng có dạng hình chữ U lật úp như đã vẽ ở trước.

            (3) Năng suất lao động trung bình đạt cực đại tại điểm năng suất lao động trung bình bằng với năng suất lao động biên:

            Năng suất lao động trung bình đạt tối đa khi:

đơn vị lao động.

            Tại điểm này, năng suất lao động trung bình là: APL = 900.000 đơn vị sản phẩm. Tại đó, năng suất lao động biên: MPL = 900.000 đơn vị sản phẩm. Vậy, tại điểm năng suất trung bình bằng với năng suất biên của lao động, năng suất trung bình đạt cực đại.

  Chúng ta vừa xem xét sự thay đổi của sản lượng, năng suất biên và năng suất trung bình của lao động ứng với một trình độ công nghệ nhất định. Theo thời gian, do có những phát minh, sáng chế làm cho trình độ công nghệ của một quá trình sản xuất được cải tiến. Qui trình sản xuất được cải tiến sẽ sử dụng đầu vào có hiệu quả hơn, tức là với cùng số lượng đầu vào như trước hay ít hơn, sản lượng được tạo ra nhiều hơn. Hình 4.2 minh họa sự tác động của việc cải tiến công nghệ đến sản lượng. Ban đầu, đường sản lượng là q₁, những cải tiến công nghệ làm đường sản lượng dịch chuyển lên trên tới đường q₂ và sau đó là q₃. Với cùng số lao động L₀, sản lượng tăng từ q₁ lên q₂ và sau đó là q₃ khi có sự cải tiến công nghệ.

Trong phần này chúng ta sẽ tìm hiểu chi tiết hơn về sự tác động của tiến bộ công nghệ đối với sản lượng. Giả sử ta có thể viết hàm sản xuất đối với một loại hàng hóa nào đó như sau:

.

            Trong đó: A(t) phản ánh các nhân tố ảnh hưởng đến sản lượng khác với lao động (L) và vốn (K). A(t) được định nghĩa là tiến bộ công nghệ theo thời gian. Ta giả sử: , nghĩa là cùng một số lượng lao động và vốn nhưng sản lượng cao hơn theo thời gian.

            Từ phương trình trên, ta có thể viết:

            Chia hai vế của đẳng thức trên cho q, ta được:

            .

            Hay là:

Như ta biết, đối với một biến số x nào đó thì   là tốc độ tăng trưởng của biến số đó trên một đơn vị thời gian. Áp dụng lý giải này vào công thức trên, ta được:

nhưng:

             hệ số co giãn của sản lượng (q) theo vốn (K) =

Tương tự:

             hệ số co giãn của sản lượng (q) theo lao động (L) = .

Tóm lại, ta có:

.

Đẳng thức này cho thấy, tốc độ tăng trưởng của sản lượng được cấu thành bởi hai nhân tố: (1) tốc độ tăng trưởng của vốn và lao động; và (2) tiến bộ công nghệ.

            Theo các nhà kinh tế, tiến bộ công nghệ ảnh hưởng đến sản lượng qua một trong ba cách sau:

1.                  Tiến bộ công nghệ trung dung:

.

Đẳng thức này cho thấy tiến bộ công nghệ có ảnh hưởng đến cả vốn và lao động Khi công nghệ sản xuất đạt đến trình độ cao hơn, cả năng suất vốn và năng suất lao động cùng được cải thiện, làm cho sản lượng cao hơn.

2.                  Tiến bộ công nghệ liên quan đến vốn:

.

Đẳng thức này cho thấy tiến bộ công nghệ chỉ ảnh hưởng đến năng suất vốn. Thí dụ, máy móc thiết bị sẽ có năng suất cao hơn khi tiến bộ công nghệ được áp dụng.

3.                  Tiến bộ công nghệ liên quan đến lao động:

.

Đẳng thức này cho biết tiến bộ công nghệ chỉ ảnh hưởng đến năng suất lao động.

  Giả sử chúng ta có các kết hợp của các yếu tố đầu vào của quá trình sản xuất vải của một doanh nghiệp được cho trong bảng 4.2 như sau.

  Bảng 4.2. Số mét vải được sản xuất ra trong ngày

Số liệu trong bảng 4.2 tuân theo quy luật năng suất biên giảm dần như đã trình bày trong phần trên. Trong bảng này, vốn được đo lường bằng số giờ sử dụng máy móc trong một ngày, còn lao động là số giờ sử dụng lao động trong sản xuất trong một ngày.

Các kết hợp đầu vào tạo ra cùng một sản lượng sẽ được biểu diễn trên một đường đẳng lượng. Thí dụ, để sản xuất ra 75 mét vải trong một ngày, doanh nghiệp có thể sử dụng các kết hợp đầu vào sau: i) 1L và 5K; ii) 2L và 3K; iii) 3L và 2K; hay 5L và 1K. Nếu chúng ta xem số giờ sử dụng lao động (L) và máy móc (K) là những đại lượng liên tục, ta có thể nhận thấy sẽ có vô số tập hợp đầu vào giữa L và K có thể cùng tạo ra 75 mét vải ngoài bốn tập hợp như đã nêu trên. Các tập hợp này sẽ cùng nằm trên một đường gọi là đường đẳng lượng.

Đường đẳng lượng cho biết các kết hợp khác nhau của vốn và lao động để sản xuất ra một số lượng sản phẩm nhất định q₀ nào đó. Như thế, ta có thể viết phương trình của đường đẳng lượng như sau:

  .                                                                                                  (4.6)

            Đường đẳng lượng tại mức sản lượng 75 mét vải có thể được vẽ như đường q₀ trong hình 4.3. Các đường q₂ và q₃ biểu diễn những mức sản lượng cao hơn như 90 và 100 mét vải. Những điểm trên đường q₀ biểu diễn tất cả những kết hợp đầu vào có thể sản xuất ra 75 mét vải một ngày, ứng với một trình độ công nghệ nhất định. Đường đẳng lượng cho thấy có rất nhiều cách để sản xuất ra một mức đầu ra nhất định. Để sản xuất ra q₀, chúng ta có thể cơ giới hóa cao độ (sử dụng nhiều vốn và ít lao động) như điểm A. Tại điểm A, doanh nghiệp sử dụng đến 5 giờ máy móc và chỉ có 1 giờ lao động. Mặt khác, chúng ta cũng có thể sử dụng nhiều lao động và ít máy móc để sản xuất ra một mức sản lượng nhất định, như điểm D. Tại đây, doanh nghiệp lại có thể sử dụng nhiều lao động (5 giờ) và ít máy móc (1 giờ)

Đường đẳng lượng có những tính chất tương tự như đường bàng quan của người tiêu dùng như đã trình bày trong Chương 3. Trong khi đường bàng quan biểu diễn những tập hợp hàng hóa tạo ra cùng một mức hữu dụng, đường đẳng lượng biểu diễn những kết hợp đầu vào khác nhau có thể tạo ra cùng một mức sản lượng. Như vậy, đẳng lượng cũng có bốn đặc trưng giống như đường bàng quan.

Các đường đẳng lượng này có các đặc điểm sau:

1.      Tất cả những phối hợp khác nhau giữa vốn và lao động trên một đường đẳng lượng sẽ sản xuất ra một số lượng sản phẩm như nhau. Chẳng hạn, hai điểm A và B trên đường đẳng lượng q₀ (ứng với số vốn là KA và số lao động là LA; số vốn là KB và số lao động là LB) sẽ cùng tạo ra mức sản lượng là q₀.

2.      Tất cả những phối hợp nằm trên đường cong phía trên (phía dưới) mang lại mức sản lượng cao hơn (thấp hơn). Chẳng hạn, các điểm nằm trên đường sản lượng q₂  sẽ mang lại mức sản lượng cao hơn các điểm nằm trên đường đường sản lượng q₁ hay q₀.

3.      Đường đẳng lượng thường dốc xuống về hướng bên phải và lồi về phía gốc tọa độ. Tính chất này có thể được giải thích bằng quy luật tỷ lệ thay thế kỹ thuật biên giảm dần.

4.      Những đường đẳng lượng không bao giờ cắt nhau.

Trên một hệ trục ta có thể vẽ ra rất nhiều đường đẳng lượng tùy theo mức sản lượng mà chúng ta cần đạt tới. Các nhà sản xuất sẽ linh hoạt sử dụng những kết hợp đầu vào tạo ra cùng một sản lượng nhưng họ sẽ chọn tập hợp có chi phí thấp nhất khi xét đến yếu tố giá của các đầu vào.

 Khi dịch chuyển dọc trên một đường đẳng lượng, ta thấy có sự thay thế giữa các yếu tố sản xuất để tạo ra một mức sản lượng không đổi. Ví dụ, di chuyển từ điểm A đến điểm B trên đường q₀, ta đã thay thế 2 đơn vị vốn bằng 1 đơn vị lao động để tạo ra 75 mét vải. Để đo lường mức độ thay thế giữa vốn và lao động, ta có khái niệm tỷ lệ thay thế kỹ thuật biên.

Khái niệm: Tỷ lệ thay thế kỹ thuật biên của vốn cho lao động  là số đơn vị vốn phải bớt đi để tăng thêm một đơn vị lao động mà không làm thay đổi tổng sản lượng.

            Ta có thể viết công thức tính tỷ lệ thay thế kỹ thuật biên như sau:

.                                                                         (4.7)

trong đó: MRTSK _{cho L} là tỷ lệ thay thế kỹ thuật biên của vốn cho lao động. Ký hiệu q = q₀ cho ta thấy là việc tính toán tỷ lệ thay thế kỹ thuật biên được thực hiện trên đường đẳng lượng q₀. Dấu trừ (-) trong công thức 4.7 để giữ cho tỷ lệ thay thế kỹ thuật biên có giá trị dương. Vì vậy, tỷ lệ thay thế kỹ thuật biên cho biết độ lớn của sự thay thế của hai đầu vào vốn và lao động. Căn cứ vào công thức này ta có thể thấy nghịch dấu với độ dốc của đường đẳng lượng tại một điểm nào đó chính là tỷ lệ thay thế kỹ thuật biên của vốn cho lao động tại điểm đó.

            Di chuyển từ điểm A đến điểm B trên đường q₀ trong hình 4.4, số lao động tăng thêm 1 đơn vị, trong khi số vốn giảm đi 2 đơn vị. Vậy tỷ lệ thay thế kỹ thuật biên là 2, nghĩa là một đơn vị lao động có thể thay thế cho hai đơn vị vốn mà không làm thay đổi sản lượng. Tương tự khi di chuyển từ điểm B đến C, tỷ lệ thay thế kỹ thuật biên là 1/1 = 1, một đơn vị lao động có thể thay thế cho 1 đơn vị vốn mà không làm thay đổi sản lượng.

Như vậy, di chuyển dọc theo đường đẳng lượng về phía phải, tỷ lệ thay thế kỹ thuật biên giảm dần. Rõ ràng, khi số lao động càng tăng lên thì năng suất biên của lao động giảm dần. Trong khi đó, số vốn giảm dần đến những đơn vị vốn có năng suất biên cao hơn. Vì vậy, số vốn cần phải giảm đi để tăng thêm một đơn vị lao động mà không làm thay đổi sản lượng sẽ giảm dần và do đó đường đẳng lượng sẽ trở nên thoải hơn. Chúng ta gọi điều này là quy luật tỷ lệ thay thế kỹ thuật biên giảm dần.

Từ quy luật tỷ lệ thay thế kỹ thuật biên giảm dần, chúng ta thấy rằng tỷ lệ thay thế kỹ thuật biên có quan hệ chặt chẽ với năng suất biên của lao động và vốn.

Khi giảm sử dụng một số lượng DK của đầu vào K, làm sản lượng giảm đi một lượng . Lượng giảm sút của sản lượng này sẽ được bù đắp bằng việc tăng sử dụng đầu vào L một lượng DL để cho sản lượng không đổi. Sản lượng tăng thêm từ việc tăng L là   phải bù đắp vừa đủ sản lượng mất đi từ việc giảm K (là ). Do vậy:

 Û .                                      (4.8)

Vì vậy, tỷ lệ thay thế kỹ thuật biên vốn của vốn cho lao động bằng với tỷ số giữa năng suất lao động biên (MPL) và năng suất vốn biên (MPK).

            Ta còn có thể chứng minh mối quan hệ này bằng phương pháp khác như sau:

Ta có hàm sản xuất:           .

Ta có thể suy ra:         .

Vì đi dọc theo một đường đẳng lượng, tổng sản lượng là không thay đổi. Do đó:     

.

            Công thức này diễn giải bằng toán học mối quan hệ nói trên.

 Thí dụ: Giả sử ta có hàm số sản xuất với dạng Cobb-Douglas như sau:

  .

 Ứng với mức tổng sản lượng q = 100 đơn vị sản phẩm, ta có:

  .

Như thế:           .

            Hay ta có thể sử dụng cách khác:

  .

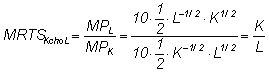            Chúng ta thấy rằng tỷ lệ thay thế kỹ thuật biên của K cho L trong trường hợp này sẽ giảm dần khi số lượng lao động được sử dụng tăng lên.

Hình dạng của đường đẳng lượng của một quá trình sản xuất phụ thuộc vào mức độ thay thế giữa vốn và lao động. Chúng ta hãy xem xét các dạng hàm sản xuất đặc biệt sau.

 Với hàm sản xuất này, khi vốn hay lao động tăng thêm một đơn vị thì sản lượng sẽ tăng thêm một lượng cố định tương ứng là a (hay b) đơn vị. Do vậy, năng suất biên của vốn hay lao động cũng chính là các hệ số a hay b. Như vậy, năng suất biên của vốn và lao động không thay đổi khi số đơn vị vốn và lao động được sử dụng tăng thêm. Do đó, đường biểu diễn mối quan hệ giữa sản lượng và mỗi yếu tố đầu vào (vốn và lao động) là các đường thẳng dốc lên có độ dốc là a hay b, nếu yếu tố đầu vào kia không đổi)

Phương trình của đường đẳng lượng ứng với hàm sản xuất tuyến tính là:

q₀ = aK + bL hay K = .

Vậy đường đẳng lượng của hàm số sản xuất này là những đường thẳng song song có độ dốc  (xem hình 4.5a).

Trong trường hợp hàm sản xuất này, vốn và lao động có thể hoàn toàn thay thế cho nhau. Nhà sản xuất có thể chỉ sử dụng vốn hay lao động cho sản xuất tùy thuộc vào giá của chúng. Tại điểm A trong hình 4.5a, để sản xuất ra mức sản lượng q₁, nhà sản xuất chỉ sử dụng vốn mà không có lao động nào. Ngược lại, tại điểm B, nhà sản xuất chỉ sử dụng lao động. Giữa hai điểm A và B, nhà sản xuất có thể sử dụng kết hợp giữa vốn và lao động. Tuy nhiên, hàm sản xuất này ít gặp trong thực tế vì ít nhất một máy móc nào đó cần có người nhấn nút hay người lao động cần được trang bị ít nhất một máy móc hay công cụ lao động nào đó.

Hàm sản xuất tuyến tính có thể thấy ở những trạm thu phí giao thông. Trong việc bán vé, nhà quản lý có thể chọn cách bán vé bằng máy tự động và không sử dụng lao động hay chỉ sử dụng người bán vé mà không sử dụng máy bán vé tự động. Ở các nước phát triển, do giá lao động thường đắt đỏ nên họ thường sử dụng máy bán vé tự động, trong khi ở nước ta, giá lao động thấp hơn nên chúng ta dùng người bán vé.

     Phương trình hàm sản xuất: q = min (aK,bL) cho biết rằng số lượng sản phẩm sản xuất ra bằng với giá trị nhỏ nhất của hai giá trị trong ngoặc.

·                    Nếu aK < bL thì q = aK. Trong trường hợp này, ta nói vốn là yếu tố ràng buộc đối với hàm sản xuất. Việc tăng thêm lao động không làm gia tăng sản lượng nên MPL= 0. Vốn là yếu tố quyết định.

·                    Nếu aK > bL thì q = bL. Trong trường hợp này, ta nói lao động là yếu tố ràng buộc đối với hàm sản xuất. Việc tăng thêm vốn không làm gia tăng sản lượng nên MPK= 0. Lao động là yếu tố quyết định.

·                    Khi aK = bL, cả hai yếu tố K và L được sử dụng tối đa. Khi đó . Đẳng thức này xảy ra tại các điểm gốc của đường đẳng lượng. Ta có thể vẽ được một đường thẳng nối các điểm gốc này (vì : đây là phương trình của một đường thẳng). Trên hình 4.5b các điểm A, B, và C là những phương án kết hợp đầu vào có hiệu quả.

Với hàm sản xuất này, vốn và lao động phải được sử dụng với một tỷ lệ nhất định, chúng không thể thay thế cho nhau. Mỗi một mức sản lượng đòi hỏi một phương án kết hợp đặc biệt giữa lao động và vốn. Trong trường hợp này, ta không thể tạo thêm sản lượng nếu như không đưa thêm vào cả vốn và lao động theo một tỷ lệ cụ thể. Do đó các đường đẳng lượng hình chữ L.

Một ví dụ về hàm sản xuất này là công việc xây dựng hè phố bê tông bằng cách sử dụng búa khoan. Mỗi búa khoan cần một công nhân điều khiển, khối lượng công việc hoàn thành chắc chắn không tăng lên khi hai người cùng sử dụng một búa hay khi một người được trang bị hai búa. Trong ngành công nghiệp may mặc, một người thợ may làm việc với một máy may. Anh ta không thể sản xuất nhiều hơn với nhiều máy may hơn. Để tăng sản lượng, số thợ may và số máy may phải tăng theo tỷ lệ tương ứng: một máy/một lao động. Loại hàm sản xuất này cũng có thể quan sát thấy trong dịch vụ taxi hay một số dịch vụ khác.

Đối với một quá trình sản xuất được đặc trưng bởi đường đẳng lượng có dạng như thế này, nhà sản xuất sẽ chọn các điểm dọc theo đường ứng với  là cố định (hình 4.5b)

     Đây là trường hợp trung gian giữa hai trường hợp trên và cũng là hàm sản xuất phổ biến nhất được áp dụng để nghiên cứu mối quan hệ giữa đầu ra và đầu vào của một quá trình sản xuất. Đường đẳng lượng của hàm sản xuất này là đường cong dốc xuống và lồi về phía gốc tọa độ (hình 4.5c). Đối với đường đẳng lượng dạng này, vốn và lao động có thể thay thế cho nhau ở một mức độ nào đó nhưng không hoàn toàn. Chẳng hạn, khi di chuyển từ điểm A đến điểm B trên đường đẳng lượng q₁, ta thay thế dần lao động cho vốn. Đường đẳng lượng dốc xuống về phía phải và tiệm cận với trục hoành nhưng không thể cắt trục hoành nên số vốn sử dụng trong sản xuất không bao giờ bằng không. Điều này có nghĩa là nhà sản xuất có thể sử dụng rất nhiều lao động để thay thế cho vốn nhưng bao giờ cũng tồn tại một lượng vốn nhất định. Ngược lại, vốn cũng có thể thay thế cho lao động khi di chuyển từ phải sang trái nhưng bao giờ cũng tồn tại một lượng lao động nhất định.

Chúng ta có thể thấy rằng một quá trình sản xuất dù tự động hóa đến đâu cũng cần có người điều khiển dây chuyền máy móc đó hay trong một ngành nghề sản xuất thủ công, người lao động cũng cần phải được trang bị một số công cụ lao động nhất định. Do vậy, đây là dạng hàm sản xuất được áp dụng phổ biến nhất trong thực tế vì nó mang những đặc điểm chung của một quá trình sản xuất.

Trong điều kiện của nền kinh tế nước ta, tình trạng dư thừa lao động ở nông thôn và thành thị xảy ra rất phổ biến nên mức tiền lương chung thấp. Đó là một lợi thế lớn của nước ta trong việc cạnh tranh thu hút vốn đầu tư nước ngoài. Các nhà sản xuất sẽ sử dụng nhiều lao động để thay thế cho vốn mà yếu tố này thường khan hiếm và đắt đỏ đối với những nước đang phát triển như nước ta. Do vậy, trong việc lựa chọn công nghệ sản xuất phù hợp với điều kiện kinh tế - xã hội, các nhà sản xuất thường ưu tiên cho các công nghệ sử dụng nhiều lao động. Với trình độ phát triển của lực lượng lao động còn thấp, nước ta chỉ nên tập trung vào phát triển các ngành hướng về xuất khẩu và sử dụng nhiều lao động như nông nghiệp và công nghiệp hàng tiêu dùng phục vụ xuất khẩu gồm dệt may, giày dép, đồ chơi, dụng cụ sinh hoạt gia đình, văn phòng phẩm, một số thiết bị điện sinh hoạt, v.v. Đó là điều mà các nước Đông Nam Á đã làm trong những năm 80 và Trung Quốc đang thực hiện (Chí, 2000).

     Một khía cạnh khác của việc đo lường tác động của sự thay đổi của cả hai yếu tố đầu vào đến sự thay đổi của sản lượng là nghiên cứu hiệu suất theo quy mô của một quá trình sản xuất. Chúng ta hãy xem xét sản lượng sẽ thay đổi như thế nào khi các đầu vào đồng loạt tăng lên theo cùng một tỷ lệ.

Nếu một hàm sản xuất có dạng q = f(K,L) và tất cả yếu tố đầu vào được nhân với một số nguyên dương cố định m (m > 1), ta phân loại hiệu suất theo quy mô của hàm sản xuất như sau:

·        Nếu sản lượng tăng lớn hơn gấp m lần, ta gọi sản xuất có hiệu suất theo quy mô tăng.

·        Nếu sản lượng tăng đúng bằng m lần, đó là sản xuất có hiệu suất theo quy mô cố định.

·        Nếu sản lượng tăng nhỏ hơn gấp m lần, ta gọi sản xuất có hiệu suất theo quy mô giảm.

Chúng ta có thể biểu diễn hiệu suất theo quy mô bằng các biểu thức như trong bảng 4.3.

 Bảng 4.3. Hiệu suất theo quy mô của sản xuất

                        Ta có thể sử dụng hàm sản xuất Cobb-Douglas để minh họa khái niệm hiệu suất theo quy mô của sản xuất. Giả sử ta có hàm sản xuất như sau:

            ,

trong đó A, a và b là các hằng số dương.

            Giả sử ta tăng số lượng các yếu tố đầu vào lên m lần . Ta sẽ có:

            .

            Nếu:

1.              thì : nếu ta tăng cả vốn và lao động lên gấp m lần thì sản lượng cũng sẽ tăng đúng bằng m lần, ta nói hàm sản xuất Cobb-Douglas có hiệu suất quy mô không đổi.

2.              thì : nếu ta tăng cả vốn và lao động lên gấp m lần thì sản lượng cũng sẽ tăng lớn hơn m lần, ta nói hàm Cobb-Douglas có hiệu suất quy mô tăng dần.

3.              thì : nếu ta tăng cả vốn và lao động lên gấp m lần thì sản lượng cũng sẽ tăng nhỏ hơn m lần, ta gọi hàm Cobb-Douglas có hiệu suất quy mô giảm dần.

Việc nghiên cứu hiệu suất theo quy mô của sản xuất giúp ích cho chúng ta điều gì? Một quá trình sản xuất có hiệu suất theo quy mô tăng có thể xảy ra do công nhân và các nhà quản lý được chuyên môn hóa cao hơn giúp họ khai thác các máy móc, thiết bị sẵn có hiệu quả hơn. Dây chuyền sản xuất xe ô-tô hay điện lực là các thí dụ cụ thể về hiệu suất theo quy mô tăng. Nếu một quá trình sản xuất có hiệu suất quy mô tăng thì chi phí sản xuất sẽ giảm vì khi đó sản lượng tăng nhanh hơn số lượng các yếu tố đầu vào.

          Các nhà lập chính sách cũng rất quan tâm đến hiệu suất theo quy mô của một quá trình sản xuất. Nếu quá trình sản xuất có hiệu suất theo quy mô tăng thì việc tổ chức một doanh nghiệp sản xuất lớn sẽ có hiệu quả kinh tế hơn nhiều so với nhiều doanh nghiệp nhỏ. Chẳng hạn, hiệu suất theo quy mô tăng trong ngành điện lực giải thích lý do vì sao chúng ta lại có những công ty điện lực lớn và chịu sự điều tiết của chính phủ.

          Trong trường hợp hiệu suất theo quy mô cố định, quy mô của doanh nghiệp không ảnh hưởng đến năng suất của các đầu vào. Năng suất trung bình và năng suất biên không thay đổi cho dù nhà máy lớn hay nhỏ. Các doanh nghiệp nhỏ cũng có thể có hiệu quả như các doanh nghiệp lớn.

          Cuối cùng, một quá trình sản xuất có hiệu suất theo quy mô giảm thường xảy ra đối với các doanh nghiệp có quy mô lớn. Những khó khăn về quản lý sẽ phát sinh khi quy mô của doanh nghiệp tăng vượt quá khả năng quản lý của ban giám đốc. Điều này có thể làm giảm năng suất của các yếu tố sản xuất do nhà quản lý không thể quan tâm đúng mức đến việc sử dụng tất cả các đầu vào. Do vậy, các doanh nghiệp có quy mô vừa và nhỏ sẽ hoạt động hiệu quả hơn các doanh nghiệp lớn.

          Chúng ta có thể minh họa những điều trên bằng việc xem xét sự thay đổi của năng suất lao động trung bình (APL) khi tăng các yếu tố đầu vào của các hàm sản xuất có hiệu suất theo quy mô khác nhau. Ta có công thức tính năng suất trung bình như sau:

            APL = .

Khi tăng vốn và lao động gấp m lần, thì năng suất lao động trung bình, lúc này, thành:

            APL' = .

1.      Trường hợp hàm sản xuất có hiệu suất theo quy mô tăng, ta có: f(mK, mL) > mf(K, L). Do vậy, APL' > APL, có nghĩa là khi ta tăng các yếu tố đầu lên thì năng suất lao động trung bình cũng tăng lên. Điều này có thể làm giảm chi phí để sản xuất ra một sản phẩm.

2.      Trường hợp hàm sản xuất có hiệu suất theo quy mô cố định, ta có: f(mK, mL) = mf(K, L). Do vậy, APL' = APL, có nghĩa là khi ta tăng các yếu tố đầu lên thì năng suất lao động trung bình không đổi và như vậy chi phí sản xuất ra một sản phẩm sẽ không đổi.

3.      Trường hợp hàm sản xuất có hiệu suất theo quy mô giảm, ta có: f(mK, mL) < mf(K, L). Do vậy, APL' < APL, có nghĩa là khi ta tăng các yếu tố đầu lên thì năng suất lao động trung bình sẽ giảm xuống. Điều này có thể làm tăng chi phí sản xuất.

 Bây giờ, chúng ta bắt đầu đề cập đến vấn đề chi phí của việc sử dụng các đầu vào: vốn và lao động. Giả sử một doanh nghiệp dùng một số tiền nào đó để mua hay thuê vốn và lao động cho sản xuất. Giả sử ta ký hiệu số tiền này là TC (tổng chi phí). Nếu đơn giá của vốn là v và của lao động là w thì doanh nghiệp có thể mua được bao nhiêu vốn và lao động. Đường đẳng phí sẽ cho ta biết điều đó.

Đường đẳng phí cho biết các kết hợp khác nhau của lao động (L) và vốn (K) có thể mua được bằng một số tiền (tổng chi phí) nhất định ứng với những mức giá nhất định.

Phương trình đường đẳng phí có dạng như sau:

TC = vK + wL .                                                                                                             (4.9)

Trong đó: TC là tổng chi phí; v là đơn giá vốn và w là đơn giá lao động.

Phương trình 4.9 cho biết tổng số tiền chi cho vốn (vK) và lao động (wL) bằng với tổng số tiền sẵn có (TC). Với một số tiền nhất định, doanh nghiệp mua nhiều lao động (hay vốn) hơn thì lượng vốn (hay lao động) mua được sẽ giảm đi. Điều này cho thấy một sự đánh đổi trong việc phân bổ chi tiêu giữa hai đầu vào. Do vậy, đường đẳng phí có dạng như hình 4.6.

Sự đánh đổi giữa vốn và lao động được biểu diễn thông qua độ dốc của đường đẳng phí. Nếu gọi S là độ dốc của đường đẳng phí, ta có:

.                                                                                         (4.10)

Công thức (4.10) cho thấy, S bằng với nghịch dấu của tỷ số giữa đơn giá của lao động và vốn và không phụ thuộc vào tổng chi phí. Do vậy, khi giá của các đầu vào thay đổi (không cùng tỷ lệ) thì độ dốc của đường đẳng phí thay đổi. Giống như đường ngân sách của người tiêu dùng trong chương 3, khi đơn giá của lao động thay đổi thì đường đẳng phí sẽ quay quanh điểm A trong hình 4.6. Khi tổng chi phí tăng, đường đẳng phí sẽ tịnh tiến về phía phải và ngược lại khi tổng chi phí giảm nó sẽ dịch chuyển về phía trái.

  Nếu như người tiêu dùng tối đa hóa hữu dụng trong điều kiện ràng buộc của ngân sách thì nhà sản xuất cũng muốn tối đa hóa sản lượng trong điều kiện ràng buộc của chi phí. Doanh nghiệp thường mong muốn đạt được sản lượng tối đa ứng với một khoản chi phí nhất định. Đây là một khía cạnh của hành vi tối đa hóa lợi nhuận của doanh nghiệp, thông qua đó xã hội có thể sử dụng tài nguyên cho sản xuất có hiệu quả. Vậy doanh nghiệp sẽ lựa chọn phối hợp đầu vào nào để tối đa hóa sản lượng?

Giả sử doanh nghiệp có phương trình đường đẳng phí như (4.9) và hàm sản xuất như (4.1). Doanh nghiệp sẽ lựa chọn tập hợp đầu vào vốn và lao động để tối đa hóa sản lượng trong điều kiện ràng buộc của chi phí. Ta có thể dùng phương pháp Lagrange để tìm ra nguyên tắc tối đa hóa sản lượng.

Phương trình (4.9) có thể viết lại như sau:

.                                                                                                         

Hàm số Lagrange có dạng:

= f(K,L) + l( vK + wL - TC) .                                                                                     

trong đó: l ¹ 0 là hệ số Lagrange. Ta cho đạo hàm riêng của theo các biến K, L và l bằng không:

,                                                                                                            

.                                                                                                 

Chuyển vế thành phần có giá đầu vào sang vế phải và lập tỷ số, ta được:

                                                                                  (4.11)  

Nguyên tắc tối đa hóa sản lượng có thể được biểu diễn qua hình 4.7. Tại điểm C, đường đẳng phí tiếp xúc với đường đẳng lượng q₁, ta thấy điểm C chính là sự lựa chọn của nhà sản xuất khi họ có số tiền là TC. Thật vậy, tại điểm C, đường ngân sách tiếp xúc tại một điểm về phía bên trái của đường đẳng lượng q₁ nên nó không thể vươn tới một đường đẳng lượng nào cao hơn nằm về phía phải của đường q₁. Vậy q₁ là đường đẳng lượng cao nhất mà đường đẳng phí đạt tới. Nó chính là mức sản lượng tối đa có thể sản xuất ra được từ số tiền TC sẳn có.

Tại điểm C, độ dốc của đường đẳng lượng bằng với độ dốc của đường đẳng phí, hay nói cách khác tỷ lệ thay thế kỹ thuật biên bằng với tỷ giá của lao động và vốn.

Ví dụ. Giả sử ta có hàm sản xuất dạng Cobb-Douglas như sau:

.

Đơn giá vốn là v đơn vị tiền; đơn giá lao động là w đơn vị tiền.

            Giả sử doanh nghiệp chỉ muốn chi ra số tiền là TC₀, hãy xác định sản lượng tối đa?

Bài giải.

Căn cứ vào bài, ta có thể viết được hàm chi phí sản xuất như sau:

.

            Để giải bài toán, ta thiết lập hàm Lagrange như sau:

.

Lấy đạo hàm của hàm số Lagrange này theo K, L và  và cho các đạo hàm này bằng không, ta được:

Lấy hai đẳng thức đầu chia cho nhau, ta được:

Nếu như w = v = 4 đơn vị tiền: phương trình này cho biết là để tối qua hóa sản lượng, ta nên chi phí cho lao động và tiền vốn với số tiền bằng nhau. Thí dụ, K = L = 4 đơn vị. Khi đó, ta sẽ sản xuất được 40 đơn vị sản phẩm và chi phí sẽ là 32 đơn vị tiền.

            Tất cả các kết hợp khác giữa vốn và lao động đều cho ra sản lượng thấp hơn. Thí dụ: K = 6 đơn vị vốn và L = 2 đơn vị lao động. Khi đó, tổng chi phí là 32 đơn vị tiền, nhưng sản lượng sẽ là:

 Một khía cạnh khác của việc tối đa hóa lợi nhuận là các doanh nghiệp tìm kiếm một phương thức sản xuất ra một mức sản lượng nhất định có chi phí thấp nhất. Bất cứ một doanh nghiệp nào cũng tìm kiếm kỹ thuật sản xuất với chi phí thấp nhất với khối lượng đầu ra cho trước hay tối đa hóa lợi nhuận với chi phí cho trước, vì giảm một đồng chi phí có nghĩa là tăng một đồng lợi nhuận. Sản xuất với chi phí thấp nhất sẽ mang lại lợi nhuận cao nhất cho doanh nghiệp.

Hình 4.8 mô tả nguyên tắc tối thiểu hóa chi phí của doanh nghiệp. Giả sử doanh nghiệp xác định cần phải sản xuất ra một mức sản lượng q₀ nhất định, đường đẳng lượng ở mức sản lượng q₀ cho biết tất cả tập hợp đầu vào có thể tạo ra q₀. Doanh nghiệp sẽ chọn sản xuất tại một điểm trên đường này có chi phí thấp nhất. Nếu giá của vốn là v và của lao động là w, một tập hợp gồm ba đường đẳng phí TC₁, TC₂, và TC₃ sẽ có cùng độ dốc là -w/v. Tương tự như việc tối đa hóa sản lượng, ta cũng nhận thấy tại điểm C, đường đẳng lượng q₀ tiếp xúc với đường đẳng phí TC₂, tập hợp đầu vào có chi phí thấp nhất và TC₂ là chi phí thấp nhất để sản xuất ra sản lượng q₀.

Nguyên tắc. Để tối thiểu hóa chi phí sản xuất để sản xuất ra một số lượng sản phẩm nhất định nào đó, nhà sản xuất sẽ chọn sản xuất tại điểm mà tỷ lệ thay thế kỹ thuật biên (giữa lao động và vốn) bằng với tỷ lệ giữa đơn giá lao động và đơn giá vốn.

            Công thức:                              

Ta cũng có thể chứng minh nguyên tắc này bằng phương pháp Lagrange. Ta cần tối thiểu hóa hàm chi phí sản xuất: TC = vK + wL, để đạt được mức sản lượng:

.

Để giải bài toán này, ta xây dựng hàm số Lagrange như sau:

Lấy đạo hàm bậc nhất của hàm số Lagrange theo L, K, và , ta có:

     [1]

    [2]

Chia [1] cho [2], ta được:        

Ví dụ: Một doanh nghiệp có hàm sản xuất: q = f(K,L) = K^1/2L^1/2. Giả sử doanh nghiệp cần sản xuất ra 100 sản phẩm. Vậy doanh nghiệp sẽ lựa chọn tập hợp đầu vào nào nếu giá của vốn là 20 và của lao động là 5 đơn vị tiền?

            Phương trình của đường đẳng lượng ở mức sản lượng là 100:

            .                                                                                                   (1)

            Để tối thiểu hóa chi phí, doanh nghiệp cần chọn tập hợp đầu vào sao cho:

            .                                                                                                           (2)              

            trong đó:          

Þ                .

Vậy công thức trên có thể được viết là:

                        .                

Thế (2) vào (1), ta được:

 và .

Doanh nghiệp sẽ sử dụng tập hợp 200L và 50K để sản xuất ra 100 sản phẩm. Khi đó, chi phí thấp nhất sẽ là:  đơn vị tiền.

PHẦN II 

LÝ THUYẾT VỀ CHI PHÍ SẢN XUẤT

 Trong phần trước, chúng ta đã xem xét mối quan hệ giữa số lượng yếu tố đầu vào và đầu ra của doanh nghiệp ở một trình độ công nghệ nhất định. Chúng ta tiếp tục phát triển lý thuyết về cung bằng việc khảo sát chi phí sản xuất. Chúng ta sẽ thấy rằng chi phí tối thiểu để sản xuất ra một mức sản lượng nhất định sẽ phụ thuộc vào sản lượng như thế nào. Chúng ta bắt đầu bằng việc tìm hiểu các khái niệm, cách xác định và đo lường chi phí sản xuất.

            Doanh thu của doanh nghiệp (TR) là khoản tiền mà doanh nghiệp kiếm được từ việc bán hàng hóa dịch vụ trong một khoảng thời gian nhất định.

Chi phí sản xuất của doanh nghiệp (TC) là các khoản phí mà doanh nghiệp gánh chịu khi sản xuất hàng hóa, dịch vụ trong một khoảng thời gian nào đó.

Lợi nhuận (p) là phần chênh lệch giữa doanh thu và chi phí sản xuất của doanh nghiệp.

            Mặc dù khái niệm về chi phí trên rất đơn giản, trong thực tế, tính toán chi phí cho những doanh nghiệp lớn rất phức tạp. Chúng ta sẽ xem xét một cách chi tiết về các khía cạnh phức tạp hơn của chi phí sản xuất mà các nhà kế toán và kinh tế quan tâm.

     Các nhà kinh tế và kế toán có những quan điểm khác nhau về chi phí và lợi nhuận của doanh nghiệp. Trong khi nhà kế toán quan tâm đến việc phản ánh những khoản thu chi thật sự của doanh nghiệp, nhà kinh tế lại quan tâm vai trò của chi phí và lợi nhuận như là yếu tố quyết định đến quyết định cung của doanh nghiệp, sự phân bổ tài nguyên cho những hoạt động cụ thể. Các nhà kinh tế chỉ ra chi phí của việc sử dụng tài nguyên không phải chỉ là những khoản chi thật sự của doanh nghiệp mà còn là chi phí cơ hội của nó.

Chi phí kế toán (tài chính) là những khoản phí tổn mà doanh nghiệp thực sự gánh chịu khi sản xuất ra hàng hóa hay dịch vụ trong một thời kỳ nhất định. Đó là những khoản phí bằng tiền dùng trang trải cho hoạt động của doanh nghiệp.

Chúng ta hãy nhìn vào bảng báo cáo thu nhập của một quán phở "Ngon miệng" trong một tháng hoạt động để tìm hiểu cách xác định các khoản doanh thu, chi phí và lợi nhuận của doanh nghiệp.

Chi phí cơ hội là khoản bị mất mát do không sử dụng nguồn tài nguyên (lao động hay vốn) theo phương thức sử dụng tốt nhất.

Để cho thấy chi phí cơ hội là thước đo đúng đắn của chi phí, chúng ta xem xét trường hợp sau. Theo ví dụ trong bảng 4.4, chủ quán phở sẽ thu được 2 triệu đồng tiền lãi về mặt kế toán. Liệu rằng chúng ta có thể kết luận rằng chủ quán này làm ăn đạt hiệu quả cao nhất không? Chúng ta đã bỏ qua chi phí cơ hội của sức lao động của người chủ quán này, đó là số tiền mà người này có thể kiếm được khi làm một công việc khác. Giả sử cá nhân này có lời mời làm việc tại một công ty, có mức lương là 3 triệu đồng/tháng. Vậy, việc mở quán phở đã thực sự làm mất đi của anh ta 1 triệu đồng/tháng mặc dù anh ta đạt được lợi nhuận kế toán là 2 triệu đồng. Chi phí cơ hội là động cơ của cá nhân khi lựa chọn công việc cho mình, chứ không phải là những khoản chi kế toán thực sự phát sinh.

Chi phí cơ hội phải được tính toán đến. Trong việc tính toán lợi nhuận kế toán, bạn không đề cập đến chi phí của việc sử dụng vốn nếu nó là vốn tự có. Số vốn đó lẽ ra có thể được dùng theo cách khác như gởi vào ngân hàng để thu được lãi suất ngân hàng hay dùng mua cổ phiếu để được cổ tức chẳng hạn. Chi phí cơ hội của vốn được bao gồm trong chi phí kinh tế của doanh nghiệp chứ không phải trong chi phí kế toán.

Chi phí kinh tế bao gồm chi phí kế toán và cả chi phí cơ hội của vốn và lao động. Sau khi khấu trừ chi phí kinh tế mà doanh nghiệp vẫn còn có lợi nhuận, ta gọi đó là siêu lợi nhuận hay lợi nhuận kinh tế. Thông thường trong một nền kinh tế, người ta lấy lãi suất ngân hàng làm thước đo chi phí cơ hội cho các khoản đầu tư vì đó là mức sinh lời trung bình của nền kinh tế.

Siêu lợi nhuận, là khoản lợi nhuận thêm vào lợi nhuận mà những người chủ doanh nghiệp có thể kiếm được bằng cách gửi tiền theo lãi suất ngân hàng.

Siêu lợi nhuận là chỉ số chính xác chỉ ra mức độ hiệu quả mà doanh nghiệp đang hoạt động. Trong khi các nhà kế toán chủ yếu quan tâm đến các khoản thu, chi thực sự của công ty thì nhà kinh tế quan tâm đến chi phí cơ hội của việc đầu tư. Đó là động cơ quan trọng của doanh nghiệp trong việc quyết định phân bổ tài nguyên cho sản xuất, kinh doanh một lĩnh vực cụ thể.

  Chi phí ngắn hạn là chi phí phát sinh trong một thời kỳ mà trong đó số lượng và chất lượng của một vài đầu vào không đổi.

            Trong ngắn hạn, chi phí cho một số đầu vào dành cho sản xuất của doanh nghiệp là cố định, trong khi chi phí cho các yếu tố đầu vào khác có thể biến đổi khi doanh nghiệp thay đổi mức sản lượng của mình. Trên cơ sở này, chúng ta có thể phân biệt những thước đo chi phí sản xuất khác nhau.

  Tổng chi phí (TC) là toàn bộ chi phí để sản xuất ra một số lượng sản phẩm q nhất định. Tổng chi phí gồm hai bộ phận cấu thành: chi phí cố định hay còn gọi là định phí và chi phí biến đổi hay còn gọi là biến phí.

Chi phí cố định (FC) là những khoản chi phí không thay đổi khi sản lượng thay đổi. Nói rộng ra, chi phí cố định là những chi phí mà doanh nghiệp phải trả dù không sản xuất một sản phẩm nào. Tùy theo loại hình sản xuất mà định phí có thể là tiền thuê mặt bằng, thuê nhà máy, khấu hao máy móc, thiết bị, tiền mua bảo hiểm và cũng có thể là tiền lương, v.v. Chi phí cố định là khoản phí mà doanh nghiệp buộc phải bỏ ra khi muốn tiến hành sản xuất và ngay cả trong khoảng thời gian nào đó mà doanh nghiệp không sản xuất, họ vẫn phải chịu khoản phí này.

Chi phí biến đổi (VC) là những khoản chi phí tăng giảm cùng với mức tăng giảm của sản lượng. Chi phí biến đổi có thể gồm các khoản chi phí: nhiên liệu, nguyên, vật liệu, tiền lương theo sản phẩm, v.v. Những khoản phí này sẽ tăng lên khi sản lượng tăng. Doanh nghiệp không phải trả những khoản phí này khi họ không sản xuất. Như vậy:

  .                                                                      (4.12)

  Sự biến đổi của tổng chi phí là do sự biến đổi của các chi phí biến đổi và khi sản lượng bằng không (không sản xuất), tổng chi phí bằng chi phí cố định.

Để quyết định sản xuất bao nhiêu, những người quản lý cần biết biến phí sẽ thay đổi như thế nào khi sản lượng tăng lên. Bên cạnh đó, họ cũng cần biết thêm về một số thước đo khác sẽ được trình bày trong phần sau.  

  Bảng 4.4 trình bày chi phí sản xuất ra 3.000 tô phở. Nếu chúng ta gộp thuế vào những khoản chi phí phải trả của quán thì tổng chi phí để làm ra 3.000 tô phở là 10.000.000 đồng. Vậy, để làm ra một tô phở chủ quán phải chi một khoản trung bình là 3.333 đồng/tô. Ta gọi 3.333 đồng là chi phí trung bình của một tô phở.

Chi phí trung bình là tổng chi phí tính trên một đơn vị sản phẩm. Như vậy hàm chi phí trung bình có dạng:

AC = .                                                                                                          (4.13)

Ta có thể xem xét công thức (4.15) chi tiết hơn:

.                                                          (4.14)

trong đó: AC là chi phí trung bình để sản xuất ra một sản phẩm. AFC là chi phí cố định trung bình. Chi phí cố định trung bình phản ánh lượng chi phí cố định trong một sản phẩm. Ví dụ, chi phí trung bình của một tô phở là 3.333 đồng, trong đó có 1.333 đồng là chi phí cố định. AVC là chi phí biến đổi trung bình, nó cho biết lượng chi phí biến đổi trong một đơn vị sản phẩm. Trong ví dụ trên, chi phí biến đổi trung bình là 2.000 đồng.

Chúng ta thấy rằng khi sản lượng sản xuất ra tăng, AFC giảm. Điều đó có thể làm giảm chi phí trung bình. Vì vậy, người ta luôn tìm cách sử dụng hết công suất nhà máy, máy móc thiết bị để giảm chi phí trung bình cho 1 đơn vị sản phẩm.

Chúng ta hãy xem xét chi phí sản xuất của quán phở "Ngon miệng" ở những mức sản lượng khác nhau trong bảng 4.5.

            Cột thứ năm trong bảng 4.5 mô tả chi phí biên của sản xuất phở tại các mức sản lượng. Nó cho chúng ta biết doanh nghiệp phải tốn thêm bao nhiêu tiền để sản xuất thêm một đơn vị sản phẩm.

            Chi phí biên là số chi phí tăng thêm do sản xuất thêm một đơn vị sản phẩm.

Vì định phí không thay đổi khi mức sản lượng của doanh nghiệp thay đổi nên chi phí biên thực ra là lượng biến phí tăng thêm do sản xuất thêm một đơn vị sản phẩm. Vì vậy, hàm chi phí biên có dạng:

.                                                            (4.15)

trong đó: MC là chi phí biên để sản xuất ra một sản phẩm.

Bảng 4.5. Các chi phí ngắn hạn của "Ngon miệng"

Ghi chú: Đơn vị tính của sản lượng là ngàn tô và của các loại chi phí là ngàn đồng.

Chi phí biên chính là đạo hàm của hàm số tổng chi phí theo sản lượng, hay là độ dốc của đường tổng chi phí.

  Nhìn vào cột chi phí biên (cột 5), chúng ta thấy chi phí biên lúc bắt đầu sản xuất cao, sau đó giảm xuống và sau đó lại tăng lên. Như vậy, đường chi phí biên có hình chữ U: lúc đầu cao, sau đó giảm rồi lại tăng như trong hình 4.10.

Ở mức sản lượng thấp, doanh nghiệp cũng phải trang trải tất cả những khoản chi phí cần thiết cho sản xuất nên phần chi phí tăng thêm (chi phí biên) rất cao. Chẳng hạn, chủ quán phở phải mua một số lượng vật liệu nhất định (bàn ghế, bánh phở, thịt, rau, v.v). Khi sản lượng tăng thêm, doanh nghiệp có thể tận dụng những đầu vào có sẵn từ việc sản xuất những sản phẩm trước đó nên phần chi phí tăng thêm sẽ giảm dần. Những sản phẩm tiếp theo sẽ có chi phí thấp hơn nên chi phí biên giảm dần. Tuy nhiên, khi sản lượng tăng đến một mức nào đó, khó khăn trong quản lý một doanh nghiệp lớn sẽ có thể xuất hiện. Năng suất của vốn và lao động dần dần giảm đi do việc sử dụng kém hiệu quả. Bây giờ, việc tăng sản lượng sẽ trở nên đắt đỏ hơn. Như vậy, chi phí bắt đầu tăng lên lại.

Hình 4.11 biểu diễn một dạng khác của đường chi phí biên. Lúc đầu, chi phí biên giảm xuống khi sản lượng tăng. Sau đó, nó không đổi khi sản lượng tăng ở bất kỳ mức nào. Mỗi đơn vị sản phẩm tăng thêm làm tăng thêm một lượng chi phí không đổi.

Hình dạng nào của đường chi phí biên thực sự được áp dụng trong thực tiễn phụ thuộc chủ yếu vào kỹ thuật sản xuất mà doanh nghiệp đang có. Hình dạng đường chi phí biên sẽ khác nhau giữa các ngành và các doanh nghiệp.

  Theo số liệu về các chi phí trong bảng 4.5, chúng ta có các nhận xét sau về sự thay đổi của chi phí trung bình và chi phí biên.

Khi chi phí biên thấp hơn tổng chi phí trung bình (MC < AC) thì nó kéo chi phí trung bình xuống, làm cho đường chi phí trung bình dốc xuống.

Khi chi phí biên vừa bằng với chi phí trung bình (MC = AC) thì chi phí trung bình không giảm nữa và lúc đó chi phí trung bình đạt cực tiểu. Đường MC và AC giao nhau tại điểm cực tiểu của AC.

Khi MC cao hơn AC (MC > AC) thì nó sẽ đẩy AC lên, đường AC dốc lên.

Điều này có thể liên hệ với thực tế như sau: một cầu thủ ghi 3 bàn thắng trong 3 trận đấu, số bàn thắng trung bình là 1 bàn/trận. Trận tiếp theo anh ta ghi 2 bàn, số bàn ghi thêm lớn hơn số trung bình ban đầu làm cho số bàn trung bình sau tăng lên thành 1,25. Trận tiếp nữa anh ta chỉ ghi thêm 1 bàn, ít hơn số bàn trung bình trước đó, số bàn trung bình sau sẽ giảm xuống thành 1,2.

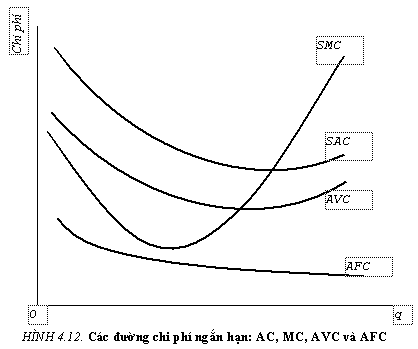
            Những hàm chi phí cụ thể có thể có nhiều hình dạng khác nhau. Hình dạng phổ biến của đường chi phí bao hàm những giả định chung về chi phí được trình bày trong hình 4.9. Đường tổng chi phí thường có dạng hàm số bậc ba theo sản lượng. AC, AVC, và MC đều là những đường cong bậc hai mà trước tiên, chúng giảm xuống và sau đó lại tăng khi sản lượng tăng. MC đạt cực tiểu trước AC và AVC, và AVC đạt cực tiểu trước khi AC đạt cực tiểu. Đường MC đi qua điểm cực tiểu của đường AVC và AC. Đường AFC luôn có dạng đường hyperbol dốc xuống bất chấp hình dạng của các đường khác. Khoảng cách theo chiều đứng giữa đường AC và AVC bằng với độ lớn của AFC và do đó giảm dần khi sản lượng tăng.

  Dài hạn là khoảng thời gian đủ dài để cho doanh nghiệp số lượng hay các loại yếu tố đầu vào của mình theo sự thay đổi của điều kiện sản xuất.

Trong dài hạn, doanh nghiệp có thể thay đổi tất cả yếu tố đầu vào của mình. Chẳng hạn, doanh nghiệp có thể thay đổi quy mô của nhà máy, chuyển sang công nghệ sản xuất mới, mướn nhân công mới và thương lượng những hợp đồng mới với các nhà cung ứng vật tư, v.v. Do vậy, trong dài hạn, doanh nghiệp có thể lựa chọn các đầu vào và công nghệ sản xuất có chi phí thấp nhất. Đường tổng chi phí dài hạn (LTC) mô tả chi phí tối thiểu cho việc sản xuất ra mỗi mức sản lượng, khi doanh nghiệp có khả năng điều chỉnh tất cả các đầu vào của mình một cách tối ưu. Bởi vì doanh nghiệp có thể đóng cửa hoàn toàn trong dài hạn nên LTC ở mức sản lượng 0 là 0. Như vậy, không có chi phí cố định trong dài hạn và mọi chi phí đều là chi phí biến đổi.

Điểm khác biệt cơ bản giữa dài hạn và ngắn hạn là sự linh động. Trong dài hạn, nhà sản xuất có thể linh động điều tiết sản lượng và chi phí bằng cách thay đổi quy mô nhà máy.

  Tương tự như trong ngắn hạn, ta cũng có các khái niệm về chi phí trung bình, và chi phí biên trong dài hạn. Trong dài hạn, ta có thể đóng cửa nhà máy nên tổng chi phí ở sản lượng bằng không là 0. Đường LAC cũng có dạng chữ U giống SAC nhưng chi phí ở mỗi mức sản lượng thấp hơn. Doanh nghiệp có thể chọn phương thức sản xuất có chi phí trung bình thấp nhất của đường SAC.

Hình 4.13 mô tả sự hình thành của đường LAC từ các đường SAC. Do trong dài hạn doanh nghiệp có thể chọn cách sản xuất có chi phí thấp nhất ở mỗi mức sản lượng nên đường LAC là tập hợp các điểm thấp nhất của các đường SAC. Đường LAC thoải hơn các đường SAC và cũng có dạng hình chữ U.

Đường chi phí biên dài hạn (LMC) cũng mô tả chi phí tăng thêm khi sản xuất thêm một đơn vị sản phẩm. Đường LMC không phải là đường tập hợp các điểm của các đường ngắn hạn. Khi LMC thấp hơn LAC, LAC sẽ giảm xuống. Tương tự, khi LMC lớn hơn LAC thì LAC tăng lên. Khi LAC đạt cực tiểu hay LAC không đổi, LMC bằng với LAC.

  Đường LAC trong hình 4.13 có dạng hình chữ U. Hình dạng này của đường LAC cho thấy LAC ban đầu cao, sau đó giảm dần và cuối cùng lại tăng. Để xem hình dạng chữ U này có ý nghĩa gì trong thực tế, chúng ta hãy xem xét khái niệm về “tính kinh tế theo quy mô”

·        Khi doanh nghiệp tăng sản lượng mà làm cho chi phí trung bình dài hạn của doanh nghiệp giảm, ta gọi quá trình sản xuất này có tính kinh tế nhờ quy mô.

·        Khi doanh nghiệp tăng sản lượng mà làm cho chi phí trung bình dài hạn của doanh nghiệp vẫn không đổi, ta gọi quá trình sản xuất này có lợi tức theo quy mô cố định;

·        Khi doanh nghiệp tăng sản lượng mà làm cho chi phí trung bình dài hạn của doanh nghiệp tăng, ta gọi quá trình sản xuất này có tính phi kinh tế vì quy mô.

Trong hình 4.14, đường LAC có tính kinh tế nhờ quy mô cho đến điểm A, nơi mà chi phí trung bình thấp nhất. Tại những mức sản lượng cao hơn, ta thấy xuất hiện tính phi kinh tế vì quy mô. Tính kinh tế theo quy mô của một quá trình sản xuất tùy thuộc vào việc: doanh nghiệp sẽ sử dụng nhiều hơn hay ít hơn đầu vào để sản xuất ra một sản phẩm khi sản lượng gia tăng? Vấn đề này phụ thuộc vào công nghệ sản xuất. Tính kinh tế theo quy mô bắt nguồn từ hiệu suất theo quy mô của sản xuất. Hiệu suất theo quy mô tăng sẽ dẫn đến tính kinh tế nhờ quy mô bởi vì doanh nghiệp có thể tăng gấp đôi sản lượng trong khi chi phí tăng chưa đến gấp đôi, làm cho chi phí trên một đơn vị sản phẩm giảm. Ngược lại, hiệu suất theo quy giảm tương ứng với tính phi kinh tế vì quy mô. Ta có thể chứng minh mối quan hệ giữa hiệu suất theo quy mô và tính kinh tế theo quy mô của quá trình sản xuất thông qua mối quan hệ giữa số lượng yếu tố đầu vào, sản lượng và chi phí trung bình.

Giả sử một quá trình sản xuất có mối quan hệ giữa số lượng yếu tố đầu vào và số lượng đầu ra được biểu thị bằng hàm sản xuất:

            q = f(K, L).

Như vậy, với số lượng yếu tố đầu vào là K và L, doanh nghiệp có thể sản xuất ra mức sản lượng q và tốn tổng chi phí TC (TC = vK + wL). Khi đó, chi phí trung bình để sản xuất ra một đơn vị sản phẩm là AC = TC/q. Khi doanh nghiệp tăng số lượng K và L lên gấp m lần, tổng chi phí sẽ tăng lên đúng gấp m lần thành mTC, còn sản lượng tăng lên thành q'.

Nếu quá trình sản xuất này có hiệu suất theo quy mô tăng, tức là q' > mq, khi đó chi phí trung bình:

AC' = .                                                               (4.16)

Theo những nghiên cứu về sản xuất lúa gạo ở nước ta, một hộ nông dân sản xuất có tính kinh tế nhờ quy mô khi quy mô đất đai không quá 2 hecta. Vượt quá 2 hecta, sản xuất trở nên phi kinh tế vì quy mô (Phương, 1997; Thông, 1998). Điều này có thể được giải thích dựa vào trình độ kỹ thuật canh tác của nông dân. Nông dân có trình độ kỹ thuật thấp và khả năng quản lý kém nên họ chỉ có khả năng sản xuất tốt trên một diện tích đất đai nhỏ. Khi diện tích đất đai lớn dần, sẽ xuất hiện những vấn đề của sản xuất lớn mà nông dân không quản lý và điều tiết có hiệu quả. Tính phi kinh tế vì quy mô xuất hiện khi diện tích đất đai lớn dần. Trong sản xuất nông nghiệp, như lúa gạo, chăn nuôi, cây ăn trái, thông thường sản lượng tuân theo lợi tức cố định theo quy mô. Hàm sản xuất của những quá trình này có dạng Cobb-Douglas mà tổng tổng số mũ của các yếu tố đầu vào xấp xỉ 1.

            Có ba nguyên nhân tạo ra tính kinh tế nhờ quy mô. Thứ nhất là tính không thể chia cắt của quá trình sản xuất. Để có thể sản xuất, doanh nghiệp đòi hỏi phải có một số lượng tối thiểu của một số đầu vào nào đó. Đôi khi chúng ta gọi chúng là chi phí cố định, vì chúng không thay đổi khi sản lượng thay đổi. Để hoạt động, doanh nghiệp cần phải có một người quản lý, một điện thoại, một kế toán, một cuộc điều tra thị trường chẳng hạn. Doanh nghiệp không thể chỉ có nửa người quản lý, hay nửa máy điện thoại khi sản xuất một mức sản lượng thấp. Ban đầu, những chi phí này sẽ không đổi khi sản lượng tăng vì người quản lý có thể kiểm soát 2 hay 3 công nhân như nhau và cũng không cần thêm một máy điện thoại nữa. Lúc này, sản xuất có tính kinh tế nhờ quy mô vì chi phí cố định có thể được phân tán nhỏ ra cho các sản phẩm. Tuy nhiên, khi sản lượng vượt quá một mức nhất định, doanh nghiệp phải cần thêm người quản lý, điện thoại, v.v., tính kinh tế nhờ quy mô biến mất và đường LAC không giảm nữa.

            Nguyên nhân thứ hai là sự chuyên môn hóa. Một nhà kinh doanh duy nhất phải đảm trách nhiều công việc khác nhau của doanh nghiệp. Khi doanh nghiệp mở rộng và có thêm nhiều nhân viên, mỗi nhân viên có thể tập trung vào một công việc chuyên biệt và như vậy, thực hiện chúng có hiệu quả hơn. Adam Smith đã nhấn mạnh lợi ích của sự chuyên môn hóa trong tác phẩm "The Wealth of Nations" (1776).

            Thứ ba là sự tận dụng lợi thế của máy móc thiết bị. Trong thực tế, ta thường thấy có sự xuất hiện của quy tắc "hai phần ba". Khi sản lượng của nhà máy, máy móc tăng lên gấp đôi, chi phí của việc vận hành nhà máy hay máy móc chỉ tăng thêm 2/3 lần. Điều này có thể làm giảm chi phí trung bình để sản xuất ra một sản phẩm và làm xuất hiện tính kinh tế nhờ quy mô. Thí dụ, những tàu chở dầu chỉ cần tăng thêm 2/3 diện tích bề mặt khi tăng thể tích chuyên chở lên gấp đôi.

PHẦN III

 TỐI ĐA HÓA LỢI NHUẬN

VÀ QUYẾT ĐỊNH CUNG CỦA DOANH NGHIỆP

      Mục tiêu của nhà sản xuất thường là để có được lợi nhuận. Các nhà kinh tế giả định rằng các doanh nghiệp sản xuất và cung ứng hàng hóa, dịch vụ để kiếm được càng nhiều lợi nhuận càng tốt. Nói cách khác, các doanh nghiệp thường hướng tới mục tiêu tối đa hóa lợi nhuận. Có thể có một số người hoài nghi về giả định này vì cho rằng doanh nghiệp có thể theo đuổi nhiều mục tiêu khác nhau. Chẳng hạn, trong một số trường hợp, doanh nghiệp quan tâm đến việc tăng doanh thu hơn là tăng lợi nhuận. Trong một số trường hợp khác, doanh nghiệp muốn giảm thiểu những rủi ro trong hoạt động mà hy sinh một phần lợi nhuận, v.v. Xét cho cùng, những công việc đó đều nhằm mục tiêu kiếm được lợi nhuận trong dài hạn. Giả định về tối đa hóa lợi nhuận sẽ giúp ích cho chúng ta trong việc tìm hiểu quá trình cung ứng của doanh nghiệp. Trong phạm vi của môn học này, chúng ta chỉ xem xét sự tối đa hóa lợi nhuận của một doanh nghiệp sản xuất duy nhất một loại sản phẩm. Điều này có thể là khiếm khuyết bởi vì trong thực tế, một doanh nghiệp hiện đại thường sản xuất nhiều loại sản phẩm đồng thời. Tuy nhiên, mục tiêu của chúng ta là phác họa hình ảnh đơn giản về hoạt động của doanh nghiệp để tìm hiểu rõ ràng về quyết định cung ứng của các doanh nghiệp.

  Như chúng ta đã biết, lợi nhuận là chênh lệch giữa doanh thu và chi phí. Giả sử doanh nghiệp sản xuất và bán ra một số lượng sản phẩm là q ở mức giá P. Khi đó, doanh thu (TR) của doanh nghiệp sẽ là tích số của P và q. Chi phí sản xuất của doanh nghiệp cũng phụ thuộc vào mức sản lượng q. Vì vậy, lợi nhuận cũng sẽ là một đại lượng phụ thuộc vào sản lượng. Ta có thể viết công thức tính lợi nhuận như sau:

.                                                                                           (4.17)     

trong đó: p, TR, TC lần lượt là lợi nhuận, doanh thu và chi phí. Tất cả các đại lượng này đều phụ thuộc vào sản lượng q.

Doanh thu biên (MR) là phần doanh thu tăng thêm do sản xuất và tiêu thụ thêm một đơn vị sản phẩm. Do vậy:

 .                                                                                               (4.18)

  Như vậy, doanh thu biên chính là đạo hàm của hàm tổng doanh thu theo sản lượng hay về mặt đồ thị doanh thu biên chính là độ dốc của đường tổng doanh thu. Chúng ta lưu ý rằng, nhìn chung, khi doanh nghiệp muốn bán ra nhiều hơn, sản lượng tăng, giá sản phẩm sẽ giảm xuống (lưu ý là đường cầu dốc xuống từ trái sang phải). Do vậy, mức doanh thu tăng thêm từ việc bán thêm một sản phẩm sẽ giảm dần khi sản lượng tăng. Điều này dẫn đến việc đường doanh thu biên dốc xuống từ trái sang phải.

Chúng ta có thể xem xét chi tiết hơn công thức 4.18 để thấy rõ mối quan hệ giữa doanh thu biên và giá cả. Dựa vào công thức tính MR, ta có thể viết lại như sau:

  .                                                                           (4.19)

            Từ công thức (4.19), ta có các nhận xét sau:

·        Nếu số lượng hàng hóa mà doanh nghiệp bán ra không ảnh hưởng gì đến giá cả thị trường (điều này xuất hiện trong thị trường cạnh tranh hoàn hảo), khi đó: : doanh thu biên bằng với giá.

·        Nếu doanh nghiệp bán ra thêm sản phẩm làm giảm giá cả thị trường (đây là đặc điểm của thị trường độc quyền) thì :  doanh thu biên nhỏ hơn giá.

Chúng ta có thể thấy sự thay đổi của doanh thu biên qua số liệu về sản lượng và doanh thu biên của một doanh nghiệp được trình bày trong bảng 4.6. Cột doanh thu biên bao gồm các giá trị giảm dần khi sản lượng tăng. Doanh thu biên giảm vì doanh nghiệp phải giảm giá để bán ra được nhiều sản phẩm hơn. Hình dạng của đường doanh thu biên phụ thuộc vào hình dạng của đường cầu. Thông thường đường cầu dốc xuống nên đường doanh thu biên cũng dốc xuống.

  Chúng ta hãy xem xét mối quan hệ giữa sản lượng, doanh thu biên, chi phí biên của một doanh nghiệp để từ đó tìm ra nguyên tắc chung để tối đa hóa lợi nhuận của một doanh nghiệp.

Để tối đa hóa lợi nhuận, doanh nghiệp chọn mức sản lượng mà tại đó chênh lệch giữa doanh thu và chi phí là lớn nhất. Điều này có thể đạt được khi đạo hàm bậc nhất của hàm lợi nhuận bằng không.

.                                      (4.20)

Do vậy, để tối đa hóa lợi nhuận doanh nghiệp sẽ chọn mức sản lượng q*, tại đó doanh thu biên bằng với chi phí biên. Chúng ta có thể minh họa điều này bằng hình vẽ của các đường MR và MC. Hình 4.16 minh họa nguyên tắc tối đa hóa lợi nhuận của một doanh nghiệp. Đường MC có hình dạng quen thuộc, hình chữ U và đường MR là đường thẳng dốc xuống ở mọi mức sản lượng. Giao điểm của hai đường này là điểm A, tại đây MR = MC. Chúng ta tìm hiểu có phải tại mức sản lượng q* này, doanh nghiệp tối đa hóa lợi nhuận không?

Bảng 4.6. Sản lượng, doanh thu biên, chi phí biên và lợi nhuận

Ở những mức sản lượng thấp hơn q*, MR lớn hơn MC. Do đó nếu bán ra thêm một sản phẩm, doanh nghiệp sẽ tăng được lợi nhuận (hay giảm được thua lỗ) vì phần doanh thu tăng thêm lớn hơn phần chi phí tăng thêm do bán ra sản phẩm đó. Do vậy, doanh nghiệp sẽ tăng sản lượng, như được chỉ ra bằng mũi tên trong hình. Ở bên phải q*, MC lớn hơn MR. Việc tăng sản lượng sẽ làm tăng thêm chi phí nhiều hơn phần tăng doanh thu. Sản xuất và bán ra thêm một sản phẩm sẽ làm giảm lợi nhuận (hay thêm thua lỗ). Như vậy, doanh nghiệp sẽ tăng thêm lợi nhuận bằng cách giảm sản lượng. Những điều này sẽ hướng dẫn doanh nghiệp chọn mức sản lượng q*. Tại q* doanh thu biên bằng đúng chi phí biên.

Số liệu trong bảng 4.6 có thể minh họa nguyên tắc này. Ở mức sản lượng là 6, doanh nghiệp tối đa hóa lợi nhuận. Khi đó, doanh thu biên xấp xỉ chi phí biên. Do để đơn giản, ta chỉ xét những mức sản lượng là số nguyên nên MR và MC không chính xác bằng nhau

 q* trong hình 4.16 thể hiện mức sản lượng tối ưu mà doanh nghiệp cần xem xét khi ra quyết định sản xuất. Đó là mức sản lượng tối đa hóa lợi nhuận hay tối thiểu hóa lỗ lã của doanh nghiệp. Sau khi chọn sản lượng tối ưu, doanh nghiệp còn phải xem xét thêm giá và chi phí trung bình để ra quyết định về cung ứng.  

  Hình 4.17 mô tả quyết định cung ứng của doanh nghiệp trong ngắn hạn. Trước tiên, doanh nghiệp sẽ chọn mức sản lượng tối ưu là q*, nơi đường MR cắt đường MC. Sau đó, doanh nghiệp sẽ so sánh giá và chi phí trung bình để quyết định sản xuất mức sản lượng q* này không. Khi sản xuất q*, doanh nghiệp sẽ chịu khoản chi phí trung bình SAC₁ tương ứng với điểm B trên đường SAC. Trong đó, chi phí biến đổi trung bình tương ứng với điểm C trên đường SAVC, là SAVC₁.

Doanh nghiệp sẽ thu được lợi nhuận khi giá bán P lớn hơn chi phí trung bình SAC₁ và chắc chắn sẽ sản xuất sản lượng q*. Khi giá thấp hơn SAC₁, doanh nghiệp bị lỗ vì giá không đủ bù đắp chi phí. Trong ngắn hạn, nếu doanh nghiệp ngưng sản xuất, nó vẫn phải trả khoản chi phí cố định. Doanh nghiệp cần so sánh khoản lỗ khi sản xuất q* và khi không sản xuất (q = 0) để có quyết định tiếp tục sản xuất hay không.

Nếu giá nằm giữa SAVC₁ và SAC₁, doanh nghiệp bị thua lỗ vì giá thấp hơn chi phí trung bình. Tuy nhiên, do giá vẫn lớn hơn SAVC nên giá bán này có thể giúp doanh nghiệp bù đắp hoàn toàn chi phí biến đổi và dôi ra một phần để bù đắp chi phí cố định. Như vậy doanh nghiệp vẫn tiếp tục sản xuất q* vì nếu không doanh nghiệp sẽ hoàn toàn lỗ phần chi phí cố định. Khi giá thấp hơn SAVC₁, doanh nghiệp không thể bù đắp đủ chi phí biến đổi và sẽ bị lỗ thêm một phần chi phí biến đổi bên cạnh toàn bộ chi phí cố định. Doanh nghiệp tốt hơn là nên ngưng sản xuất. Mức giá bằng với SAVC₁ được gọi là mức giá bắt đầu sản xuất hay mức giá ngưng sản xuất.

     Trong sản xuất dài hạn, chi phí cố định không còn tồn tại do mọi yếu tố đầu vào đều có thể thay đổi nên ta chỉ xét tổng chi phí hay tổng chi phí trung bình LAC. Trong phần trước, ta đã biết mức sản lượng tạo ra lợi nhuận tối đa hoặc mức thua lỗ tối thiểu nằm tại điểm A (hình 4.18) với .

Khi chọn sản xuất mức sản lượng q*, doanh nghiệp sẽ chịu khoản chi phí trung bình dài hạn LAC₁. Lúc ấy doanh nghiệp phải xem xét tại mức sản lượng q*, doanh nghiệp có lãi hay bị thua lỗ. Nếu giá bán bằng hay lớn hơn LAC₁ thì doanh nghiệp không bị thua lỗ và tiếp tục sản xuất sản lượng q*. Tại mức giá bằng với LAC₁, ta gọi là mức giá hòa vốn.

Nếu giá thấp hơn LAC₁ thì doanh nghiệp sẽ ngưng hoạt động và rời khỏi ngành. Điểm khác biệt so với quyết định cung trong ngắn hạn là doanh nghiệp sẽ đóng cửa trong dài hạn khi bị lỗ. Trong dài hạn, doanh nghiệp đã chọn công nghệ sản xuất có chi phí thấp nhất ở mỗi mức sản lượng mà vẫn bị thua lỗ nên tốt hơn là nên đóng cửa. Trong khi đó, trong ngắn hạn, doanh nghiệp chỉ quyết định tạm thời ngưng sản xuất khi giá thấp hơn SAVC và sẽ tiếp tục ở lại trong ngành và cung ứng nếu điều kiện thị trường khả quan hơn.

 Bảng 4.7. Tóm tắt các quyết định của doanh nghiệp về cung ứng

             Thí dụ: Một doanh nghiệp có hàm tổng chi phí ngắn hạn như sau: . Giá bán mà doanh nghiệp nhận được phụ thuộc vào sản lượng mà hãng sản xuất ra và có dạng P = 50 - 0,1q. Hỏi doanh nghiệp sẽ sản xuất mức sản lượng là bao nhiêu để tối đa hóa lợi nhuận và khi đó lợi nhuận thu được là bao nhiêu?

            Giải: Chúng ta biết rằng doanh nghiệp cần chọn mức sản lượng mà tại đó MR=MC nên chúng ta cần xác định hàm MR và MC của doanh nghiệp.

  .           

MC = = 0,2q + 10.

 Để tối đa hóa lợi nhuận, ta có MR = MC, nên:

                         50 - 0,2q = 0,2q + 10 Û q = 100 đơn vị sản phẩm (đvsp).

 Khi đó, giá mà doanh nghiệp nhận được khi bán 100 đvsp là:

                         P = 50 - 0,1*100 = 40 đvt.

 Doanh thu của doanh nghiệp:

                         TR = 40.100 = 4000 đvt.

 Chi phí để sản xuất ra 100 đvsp:

                         TC = 0,1.100² + 10.100 + 1000 = 3.000 đvt.

 Lợi nhuận mà doanh nghiệp thu được là:

                         p = TR - TC = 4000 - 3000 = 1.000 đvt.

     Trong một số trường hợp, doanh nghiệp có thể chọn mục tiêu là tối đa hóa doanh thu trong một khoảng thời gian nhất định thay vì tối đa hóa lợi nhuận như giả định chung của chúng ta. Mục tiêu này có thể được theo đuổi bởi các doanh nghiệp mới gia nhập vào thị trường, các doanh nghiệp muốn tăng nhanh thị phần hay các doanh nghiệp muốn đạt được tính kinh tế nhờ quy mô. Coca Cola, P&G, ICI, .v.v. trong thời gian mới thâm nhập vào thị trường Việt Nam đã đưa ra mục tiêu tối đa hóa doanh thu. Các công ty này muốn bán được càng nhiều càng tốt nhằm chiếm lĩnh thị trường Việt Nam, làm cơ sở để đạt tính kinh tế nhờ quy mô sau này. Chúng ta xem xét làm thế nào để doanh nghiệp tối đa hóa được doanh thu.

            Chúng ta đã biết doanh thu của doanh nghiệp là một hàm số theo giá cả và sản lượng:

 TR = P.q.                                                                                                                 (4.21)

            Mức sản lượng mà doanh nghiệp tối đa hóa doanh thu phải thỏa mãn điều kiện:

             .                                                                                                    (4.22)

             Như vậy, để tối đa hóa doanh thu, doanh nghiệp cần chọn mức sản lượng mà tại đó doanh thu biên bằng 0.

            Thí dụ: Chúng ta trở lại thí dụ trong phần nguyên tắc tối đa hóa lợi nhuận ở trên. Giả sử doanh nghiệp muốn đạt doanh thu tối đa thay vì lợi nhuận tối đa, hỏi doanh nghiệp cần sản xuất sản lượng là bao nhiêu?

            Giải: Hàm doanh thu của doanh nghiệp:

                                     TR = P.q = (50 - 0,1q)q = 50q - 0,1q²

 Hàm doanh thu biên của doanh nghiệp:

                                                             MR = 50 - 0,2q

            Để tối đa hóa doanh thu, doanh nghiệp đặt: MR = 0.

 Û                50 - 0,2q = 0

Û                q = 250 đvsp.

 Khi đó giá bán của doanh nghiệp sẽ là:

                         P = 50 - 0,1.250 = 25 đvt.

 Doanh thu đạt được:

                         TR = 25. 250 = 6250 đvt.

 Đây là doanh thu tối đa mà doanh nghiệp có thể đạt được. Ta có thể minh họa điều này bằng đồ thị của hàm doanh thu. Vì doanh thu là hàm số bậc hai của q và hệ số của q² âm (-0,1), nên đường TR có dạng hình parabol lật úp với đỉnh là cực đại (hình 4.19).

Chi phí để sản xuất ra 250 đvsp:

                         TC = 0,1.250² + 10.250 + 1000 = 9750 đvt.

 Lợi nhuận thu được:

                                     p = TR - TC = 6250 - 9750 = -3.500 đvt.

            Nhận xét: Với mục tiêu tối đa hóa doanh thu, doanh nghiệp sản xuất mức sản lượng cao hơn so với mục tiêu tối đa hóa lợi nhuận. Đó là mức sản lượng mà doanh nghiệp có thể thu được doanh thu lớn nhất. Tuy nhiên, khi đó, giá bán của doanh nghiệp giảm đáng kể, làm cho doanh nghiệp bị lỗ 3500 đvt. Mặc dù doanh thu thu được là cao nhất nhưng do chi phí sản xuất tăng rất nhanh nên doanh nghiệp bị lỗ.

Trong thực tế, một số doanh nghiệp khi theo đuổi mục tiêu tối đa hóa doanh thu có thể chấp nhận chịu lỗ trong một khoảng thời gian nhất định. Khi đã chiếm lĩnh được thị trường và đạt được tính kinh tế nhờ quy mô, các doanh nghiệp có thể thu được lợi nhuận trong dài hạn (xem Chương 6).

Tối đa hóa lợi nhuận và tối đa hóa doanh thu. Vấn đề đặt ra là liệu rằng một doanh nghiệp có thể đồng thời theo đuổi cả hai mục tiêu: tối đa hóa lợi nhuận và tối đa hóa doanh thu hay không. Chúng ta hãy xem xét lại điều kiện để tối đa hóa lợi nhuận và tối đa hóa doanh thu để trả lời cho câu hỏi này.

Để tối đa hóa lợi nhuận, doanh nghiệp đặt: MR = MC. Trong khi đó, để tối đa hóa doanh thu, doanh nghiệp đặt: MR = 0. Ta thấy rằng hai điều kiện này sẽ cùng được thỏa mãn khi MR = MC = 0. Điều này không thể xảy ra bởi vì MC không thể bằng 0. Để sản xuất ra thêm một sản phẩm nào đó, doanh nghiệp nhất thiết phải tốn thêm tiền cho sản phẩm đó nên MC luôn luôn dương (MC > 0). Do vậy, ta có thể kết luận một doanh nghiệp không thể vừa theo đuổi mục tiêu tối đa hóa lợi nhuận, vừa theo đuổi mục tiêu tối đa hóa doanh thu. Ví dụ trên là một minh họa cho điều chúng ta vừa chứng minh. Doanh nghiệp sẽ thu được lợi nhuận tối đa là 1000 đvt khi chọn mục tiêu tối đa hóa lợi nhuận. Trong khi đó, nếu doanh nghiệp chọn mục tiêu tối đa hóa doanh thu thì doanh thu tối đa thu được là 6250 đvt. Khi đó, doanh nghiệp bị lỗ.

 Trong phần trước, chúng ta xem xét quyết định cung ứng của doanh nghiệp để tối đa hóa lợi nhuận ứng với một mức sản lượng đầu ra. Thật ra, chúng ta biết đầu ra của doanh nghiệp phụ thuộc vào yếu tố đầu vào (vốn và lao động) mà doanh nghiệp sử dụng thông qua hàm sản xuất q = f(K,L). Ngoài cách tính như đã trình bày trong phần trước, lợi nhuận còn có thể được biểu diễn như là một là hàm của các yếu tố đầu vào như sau:

  .                                                                    (4.23)

 Như vậy, doanh nghiệp cũng có thể chọn mức đầu vào để tối đa hóa lợi nhuận bằng cách chọn số lượng đầu vào sao cho đạo hàm bậc nhất của lợi nhuận trong (4.23) bằng 0:

                                                                                    (4.24)

 hay:

                                                                                                              (4.25)

 Theo (4.25) thì doanh nghiệp muốn tối đa hóa lợi nhuận sẽ phải dùng thêm yếu tố đầu vào cho đến khi doanh thu tăng thêm do sử dụng đơn vị yếu tố đó bằng với chi phí tăng thêm do sử dụng thêm đơn vị yếu tố đó.

            Doanh thu tăng thêm do sử dụng đơn vị yếu tố sản xuất nào đó được gọi là giá trị sản phẩm biên của yếu tố sản xuất đó (MRP).

                                               (4.26) 

hay tóm lại:                   .

 Chi phí tăng thêm do sử dụng thêm một đơn vị yếu tố sản xuất nào đó được gọi là chi tiêu biên.

Nếu đường cung các yếu tố đầu vào của doanh nghiệp là hoàn toàn co giãn (doanh nghiệp không có ảnh hưởng gì đến giá cả các yếu tố đầu vào, hay đường cung nằm ngang ở mức giá nhất định(1)), thì chi tiêu biên chính là giá của yếu tố đầu vào đó. Doanh nghiệp là người chấp nhận giá.

 Ta có:                                                                                              (4.27)

 Trong đó: v và w là giá của vốn và lao động. Vậy để tối đa hóa lợi nhuận thì:

                                                                                     (4.28)

 Trong trường hợp doanh nghiệp là người chấp nhận giá trên thị trường đầu ra (thị trường cạnh tranh hoàn hảo), doanh thu biên bằng với giá thị trường, đẳng thức (4.28) thành:

                                                                (4.29)

 Vế trái của đẳng thức là trường hợp đặc biệt của giá trị sản phẩm biên, trong đó khối lượng đầu ra được sản xuất ra bởi một đơn vị yếu tố đầu vào tăng thêm được định giá trị tại giá thị trường của nó.

Đẳng thức này chỉ ra một điều: để tối đa hóa lợi nhuận doanh nghiệp cần thuê mướn (sử dụng) yếu tố đầu vào cho đến khi giá trị sản phẩm biên bằng với chi phí biên của việc thuê mướn yếu tố đầu vào. Nghĩa là: doanh nghiệp cần tính toán doanh thu - chi phí cho mỗi đơn vị yếu tố đầu vào và ngưng thuê mướn khi lợi nhuận tăng thêm của yếu tố đầu vào bằng không.

            Hình 4.20 biểu diễn sự lựa chọn số lượng lao động sử dụng trong sản xuất của doanh nghiệp để tối đa hóa lợi nhuận. Giả sử số lượng lao động mà doanh nghiệp thuê trên thị trường lao động không ảnh hưởng đến giá của lao động trên thị trường, đường cung lao động (SL) sẽ là đường thẳng nằm ngang tại một mức giá w₀ nào đó. Đường giá trị sản phẩm biên của lao động sẽ dốc xuống về phía phải. Khi số lao động được sử dụng tăng lên, giá trị sản phẩm biên giảm dần do năng suất biên của lao động giảm dần.

            Doanh nghiệp sẽ sử dụng số lao động L* tương ứng với giao điểm A giữa đường SL và đường MRPL, điểm A. Tại điểm A, giá trị làm ra của người lao động cuối cùng (MRPL) bằng đúng với giá thuê của lao động (tiền công) mà doanh nghiệp phải trả. Ta thấy số lao động tối ưu mà doanh nghiệp sẽ chọn phụ thuộc vào giá tiền công. Khi tiền công thay đổi, doanh nghiệp sẽ dựa vào các điểm tương ứng trên đường MRPL để quyết định số lao động cần thuê. Vậy, các điểm trên đường MRPL biểu diễn số lao động mà doanh nghiệp sẽ sử dụng tại mỗi mức giá hay ta còn có thể gọi đường MRPL là đường cầu về lao động của doanh nghiệp. Khi tiền công tăng, lượng cầu lao động của doanh nghiệp sẽ giảm xuống và ngược lại lượng cầu sẽ tăng khi tiền công giảm.

1.                  Hãy cho một ví dụ chứng tỏ quy luật năng suất biên giảm dần của các yếu tố đầu vào?

2.                  Tại sao, trong ngắn hạn, năng suất biên của một yếu tố sản xuất ban đầu tăng và sau đó giảm sút khi số lượng yếu tố sản xuất đó tăng lên trong một quá trình sản xuất?

3.                  Khi thuê mướn thêm nhân công, người chủ doanh nghiệp nên quan tâm đến năng suất trung bình hay năng suất biên của những nhân công này?

4.                  Hãy cho ví dụ về sự thay thế giữa vốn và lao động trong một quá trình sản xuất. Nhà sản xuất nên lựa chọn tập hợp đầu vào nào để sản xuất?

5.                  Nghiên cứu hiệu suất theo quy mô của một quá trình sản xuất có ý nghĩa gì trong thực tế?

6.                  Một doanh nghiệp có thể có hàm sản xuất có hiệu suất theo quy mô tăng, cố định và giảm ở mỗi mức sử dụng đầu vào khác nhau không?

7.                  Một bạn sinh viên đại học sẽ đo lường chi phí cơ hội của thời gian học tập trong trường của mình như thế nào?

8.                  Tại sao đường chi phí biên của một doanh nghiệp thường có dạng hình chữ U?

9.                  Nếu chi phí biên của sản xuất lớn hơn biến phí trung bình thì điều này có cho bạn biết biến phí trung bình đang tăng hay giảm hay không?

10.              Hãy dùng hình vẽ để chứng minh doanh nghiệp, muốn tối đa hóa lợi nhuận, phải đặt MR = MC.

11.              Doanh nghiệp có thể đồng thời đạt được lợi nhuận tối đa và doanh thu tối đa hay không? Tại sao?

12.              Tại sao đường MRP của một yếu tố sản xuất chính là đường cầu về yếu tố đầu vào của một doanh nghiệp?

 1. Giả sử hàm sản xuất cho sản phẩm V là:

  .

 Trong đó: q là số lượng sản phẩm V, K là vốn và L là lao động.

a.       Giả sử K = 10, hãy vẽ đường năng suất lao động trung bình. Năng suất lao động trung bình tối đa tương ứng với số lượng lao động là bao nhiêu? Khi đó, số lượng sản phẩm sản xuất ra là bao nhiêu?

b.      Giả sử là K = 10, hãy vẽ đường năng suất lao động biên. Ứng với số lượng lao động là bao nhiêu thì năng suất lao động biên bằng không?

c.       Nếu K = 20, câu a và b có kết quả như thế nào?

d.      Hàm số này có hiệu suất quy mô cố định, giảm hay tăng?

2. Giả sử hàm số sản xuất của sản phẩm B có dạng như sau:

.

a.       Hãy tính năng suất lao động trung bình và năng suất vốn trung bình?

b.      Hãy vẽ đường năng suất lao động trung bình nếu K = 100?

c.       Trong trường hợp K = 100, hãy chứng tỏ là , . 

d.      Hãy vẽ các đường đẳng lượng trong trường hợp q = 100.

e.       Sử dụng kết quả ở câu c, hãy tính tỷ lệ thay thế biên dọc theo đường q = 10 tại các điểm K = L = 10; K = 25 và L = 4; và K = 4 và L = 25? Có phải là tỷ lệ thay thế kỹ thuật biên giảm dần không?

3. Giả sử ta có hàm sản xuất có dạng Cobb-Douglas như sau: 

,

 Trong đó a, b > 0 và công ty có thể sử dụng vốn và lao động trên thị trường đầu vào là cạnh tranh hoàn toàn với đơn giá là v và w.

Hãy chứng minh rằng để tối thiểu hóa chi phí, ta cần phải có:

  .

 4. Giả sử sản phẩm H được sản xuất ra theo phương trình sản xuất như sau:

 Trong ngắn hạn số vốn được cố định ở mức K = 100. Đơn giá vốn là 1 đơn vị tiền và đơn giá lao động là 4 đơn vị tiền.

a.       Hãy xác định đường tổng chi phí trong ngắn hạn? Hãy xác định đường chi phí trung bình trong ngắn hạn?

b.      Hãy xác định hàm số chi phí biên trong ngắn hạn? STC, SATC, và SMC của công ty là bao nhiêu nếu như công ty sản xuất 25, 50, 100, 200 đơn vị sản phẩm H?

c.   Đường chi phí trung bình cắt đường chi phí biên ở điểm nào? Giải thích tại sao đường MC luôn cắt đường AC tại điểm cực tiểu của AC?

5. Trong các hàm sản xuất dưới đây, hàm nào thể hiện quy luật năng suất biên giảm dần?

a. y = x^0,2         b. y = 3x          c. y = x³           d. y = 6x - 0,1x²

6. Dùng Excel để vẽ đồ thị hàm sản xuất sau: y = 0,4x + 0,09x² - 0,003x³ khi x biến đổi từ 0 đến 20. Xác định và vẽ các hàm số MP và AP tương ứng.

7. Giả sử có hàm sản xuất như sau: Y = 300 + 200F + 150P - 70F² - 20P² + 50FP

trong đó:           Y là sản lượng của một héc-ta vụ mùa,

                        F là lượng phân bón sử dụng trong năm,

                        P là số máy móc được áp dụng trên 1 héc-ta.

a.       Dùng Excel để vẽ hàm sản xuất và các đường đẳng lượng của hàm sản xuất này.

Giả sử giá một đơn vị của Y là 10, của phân là 40 và của máy móc là 25 (ngàn đồng).

b.      Số lượng đầu vào tối ưu của phân và máy móc là bao nhiêu?

c.       Tại điểm tối ưu trên, chi phí cho mỗi đầu vào là bao nhiêu và lợi nhuận là bao nhiêu?

d.      Giả sử nông dân có số vốn giới hạn và chỉ có thể chi không quá 400 ngàn đồng/ha cho hai yếu tố đầu vào. Hãy dùng phương pháp Lagrange để xác định mức đầu vào mà nông dân sẽ sử dụng. Lợi nhuận kiếm được là bao nhiêu?

e.       So sánh kết quả của hai trường hợp có ràng buộc và không ràng buộc. Giải thích.

8. Giả sử có các số liệu sau về hàm sản xuất. Giá của Y là 5 đvt và của X là 4. Điền vào chỗ trống:

Mức sử dụng đầu vào để tối đa hóa lợi nhuận là bao nhiêu? Chỉ ra điểm này bằng cách tính TR và TFC ở mỗi mức đầu vào như trong bảng.

9. Giả sử có hàm sản xuất:        Y = 138 + 0,4X - 0,002X².

a.       Doanh nghiệp sẽ sử dụng bao nhiêu X để tối đa hóa sản lượng.

b.      Doanh nghiệp sẽ sử dụng bao nhiêu X để tối đa hóa lợi nhuận nếu giá của X là 2 và của Y là 6.

c.       Lợi nhuận của doanh nghiệp là bao nhiêu ở câu b?

d.      Lợi nhuận của doanh nghiệp là bao nhiêu ở câu a?

e.       Giả sử giá của cả đầu vào và đầu ra tăng gấp đôi. Chứng minh số lượng đầu vào để tối đa hóa lợi nhuận không đổi. Lợi nhuận sẽ như thế nào? Giải thích.

10. Giả sử có hàm sản xuất:      Y = 0,4x + 0,09x² - 0,003x³

Giá của X là 20 và của Y là 25. Hãy dùng Excel để tính toán và vẽ đồ thị các đường Y, MP, AP, TR, VC, MRP, ARP khi x biến đổi từ 0 đến 20. Xác định tối đa hóa lợi nhuận.